Agencia Estatal Boletín Oficial del Estado

La Directiva 2002/49/CE del Parlamento Europeo y del Consejo, de 25 de junio de 2002, sobre evaluación y gestión del ruido ambiental, tiene como objetivo establecer un enfoque común destinado a evitar, prevenir o reducir con carácter prioritario los efectos nocivos, incluyendo las molestias, de la exposición al ruido ambiental.

Para ello, se determinará la exposición al ruido ambiental a través de la cartografía del ruido, con métodos de evaluación comunes, se garantizará la disponibilidad pública de la información relativa al ruido ambiental y a sus efectos, y, se adoptarán planes de acción basados en los resultados de la cartografía del ruido, con vistas a prevenir y reducir el ruido ambiental.

Para evaluar la exposición al ruido ambiental, la norma europea establece en su anexo II los métodos de evaluación para los indicadores de ruido contemplados en el artículo 6 de la misma. Asimismo, en su artículo 12 se contempla que la Comisión procederá a la adaptación al progreso técnico y científico, entre otros, del citado anexo II.

Esta directiva se transpuso al ordenamiento jurídico español mediante la Ley 37/2003, de 17 de noviembre, del Ruido, y dos reales decretos que la desarrollan, en concreto, el Real Decreto 1513/2005, de 16 de diciembre, por el que se desarrolla la Ley 37/2003, de 17 de noviembre, del Ruido, en lo referente a la evaluación y gestión del ruido ambiental y el Real Decreto 1367/2007, de 19 de octubre por el que se desarrolla la Ley 37/2003, de 17 de noviembre, del Ruido, en lo referente a zonificación acústica, objetivos de calidad y emisiones acústicas.

El Real Decreto 1513/2005, de 16 de diciembre, tiene por objeto la evaluación y gestión del ruido ambiental con la finalidad de prevenir, reducir o evitar los efectos nocivos, incluyendo las molestias, derivadas de la exposición al ruido ambiental, de conformidad con lo dispuesto en la Directiva 2002/49/CE del Parlamento Europeo y del Consejo, de 25 de junio de 2002. Desarrolla las previsiones legales relativas a los índices de ruido que deben considerarse en la preparación y revisión de los mapas estratégicos de ruido y que se detallan en el anexo I, así como los métodos de evaluación para la determinación de tales índices, que se especifican en el anexo II.

En julio de 2015 se publicó en el «Diario Oficial de la Unión Europea» la Directiva 2015/996 de la Comisión, de 19 de mayo de 2015, por la que se establecen métodos comunes de evaluación del ruido en virtud de la Directiva 2002/49/CE del Parlamento Europeo y del Consejo. Mediante esta nueva Directiva se sustituye el anexo II de la Directiva 2002/49/CE del Parlamento Europeo y del Consejo, de 25 de junio de 2002.

Con el objetivo de dar cumplimiento a las obligaciones del Reino de España como Estado miembro, se aprueba la presente orden, mediante la cual se transpone la Directiva (UE) 2015/996 de la Comisión al ordenamiento jurídico español, y se sustituye el anexo II del Real Decreto 1513/2005, de 16 de diciembre, para su adaptación al progreso técnico.

Con la modificación del anexo II del Real Decreto 1513/2005, de 16 de diciembre, se sustituyen los métodos de cálculo de los índices de ruido Lden y Ln utilizados actualmente para la evaluación del ruido industrial, del ruido de aeronaves, del ruido de trenes y del ruido del tráfico rodado, por una metodología común de cálculo desarrollada por la Comisión Europea a través del proyecto «Métodos comunes de evaluación del ruido en Europa (CNOSSOS-EU)». La utilización de esta metodología será vinculante para los Estados miembros a partir del 31 de diciembre de 2018, dejando pues de ser aplicables los métodos del actual anexo II que, tal y como señalan los respectivos artículos 6.2 de la Directiva 2002/49/CE y del propio Real Decreto 1513/2005, de 16 de diciembre, solo estarían en vigor en tanto no se adoptaran los métodos que ahora se establecen.

Esta orden tiene su fundamento constitucional en el artículo 149.1, apartados 16.ª y 23.ª de la Constitución, que atribuyen al Estado, respectivamente, las competencias exclusivas en materia de legislación básica sobre bases y coordinación general de la sanidad y en materia de protección del medio ambiente, sin perjuicio de las facultades de las Comunidades Autónomas de establecer normas adicionales de protección.

En virtud del artículo 13 de la Ley 37/2003, de 17 de noviembre, del Ruido, el Gobierno regulará «los métodos de evaluación para la determinación de los valores de los índices acústicos aludidos en el artículo 12 y de los correspondientes efectos de la contaminación acústica». Asimismo, de acuerdo con su disposición final segunda, se habilita al Gobierno para dictar las normas de desarrollo que requiera dicha ley. Por lo demás, a través de la habilitación contenida en la disposición final segunda, apartado 2, del Real Decreto 1513/2005, de 16 de diciembre, por el que se desarrolla la Ley 37/2003, de 17 de noviembre, del Ruido, en lo referente a evaluación y gestión del ruido ambiental, se faculta a los Ministerios de Sanidad y Consumo y de Medio Ambiente, hoy Ministerio de Sanidad, Consumo y Bienestar Social y Ministerio para la Transición Ecológica, para introducir conjunta o separadamente, según las materias de que se trate, y en el ámbito de sus competencias, cuantas modificaciones fueran precisas para mantenerlo adaptado a las innovaciones que se produzcan en la normativa europea.

Esta orden ministerial se dicta de acuerdo con los principios de buena regulación y, en concreto, con los de necesidad, eficacia, proporcionalidad, seguridad jurídica, transparencia y eficiencia, en cuanto a su contenido y tramitación, de conformidad con lo dispuesto en el artículo 129 de la Ley 39/2015, de 1 de octubre, del Procedimiento Administrativo Común de las Administraciones Públicas.

Con carácter previo a la redacción de esta norma se ha sustanciado la consulta pública regulada en el artículo 133 de la Ley 39/2015, de 1 de octubre, del Procedimiento Administrativo Común de las Administraciones Públicas, en relación con el artículo 26 de la Ley 50/1997, de 27 de noviembre, del Gobierno. En su elaboración se ha consultado a las comunidades autónomas y a las entidades representativas de los sectores afectados; asimismo, se ha sometido al trámite de información pública y se ha remitido al Consejo Asesor de Medio Ambiente, en aplicación de las previsiones de la Ley 27/2006, de 18 de julio, por la que se regulan los derechos de acceso a la información, de participación pública y de acceso a la justicia en materia de medio ambiente (incorpora las Directivas 2003/4/CE y 2003/35/CE).

En su virtud, a propuesta de las Ministras para la Transición Ecológica y de Sanidad, Consumo y Bienestar Social, de acuerdo con el Consejo de Estado, dispongo:

Artículo único. Modificación del anexo II del Real Decreto 1513/2005, de 16 de diciembre, por el que se desarrolla la Ley 37/2003, de 17 de noviembre, del Ruido, en lo referente a la evaluación del ruido ambiental.

Se substituye el contenido del anexo II del Real Decreto 1513/2005, de 16 de diciembre, por el que se desarrolla la Ley 37/2003, de 17 de noviembre, del Ruido, en lo referente a la evaluación del ruido ambiental, por el nuevo contenido del anexo incluido en esta orden.

Disposición final primera. Fundamento constitucional y carácter básico.

Esta orden se dicta al amparo de las competencias exclusivas que al Estado otorga el artículo 149.1.16.ª y 23.ª de la Constitución Española, en materia de bases y coordinación general de la sanidad y de legislación básica sobre protección del medio ambiente, sin perjuicio de las facultades de las comunidades autónomas de establecer normas adicionales de protección.

Disposición final segunda. Incorporación del Derecho de la Unión Europea.

Mediante esta orden se incorpora al Derecho español la Directiva 2015/996 de la Comisión, de 19 de mayo de 2015, por la que se establecen métodos comunes de evaluación del ruido en virtud de la Directiva 2002/49/CE del Parlamento Europeo y del Consejo.

Disposición final tercera. Entrada en vigor.

Esta orden entrará en vigor el día 31 de diciembre de 2018.

Madrid, 7 de diciembre de 2018.–La Vicepresidenta del Gobierno y Ministra de la Presidencia, Relaciones con las Cortes e Igualdad, Carmen Calvo Poyato.

ANEXO

«ANEXO II

Métodos de evaluación para los indicadores de ruido

(a los que se hace referencia en el artículo 6 del Real Decreto 1513/2005)

1. INTRODUCCIÓN.

Los valores de L_den y L_n se determinarán mediante un cálculo en el punto de evaluación, según el método estipulado en el capítulo 2 y los datos descritos en el capítulo 3. Las mediciones podrán realizarse conforme a lo estipulado en el capítulo 4.

2. MÉTODOS COMUNES PARA LA EVALUACIÓN DEL RUIDO.

2.1. Disposiciones generales – Ruido del tráfico viario, del tráfico ferroviario y ruido industrial.

2.1.1. Indicadores, gama de frecuencias y definiciones de banda.

Los cálculos de ruido se definirán en la gama de frecuencias de las bandas de octava comprendidas entre 63 Hz y 8 kHz. Los resultados de la banda de frecuencias se facilitarán en el intervalo de frecuencias correspondiente.

Los cálculos se realizan por bandas de octava para el ruido del tráfico viario, del tráfico ferroviario e industrial, salvo para la potencia sonora de la fuente de ruido ferroviario, que usa bandas de tercio de octava. En el caso del ruido del tráfico viario, del tráfico ferroviario e industrial, conforme a estos resultados de banda de octava, el nivel sonoro medio a largo plazo con ponderación A para el día, la tarde y la noche, tal y como se establece en el anexo I y en el artículo 5 de la Directiva 2002/49/CE, se calcula mediante la suma de todas las frecuencias.

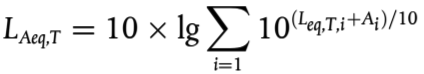
(2.1.1)

Donde:

A_i indica la corrección con ponderación A según la norma CEI 61672-1

i = índice de la banda de frecuencias

y T es el período de tiempo correspondiente al día, la tarde o la noche.

Parámetros del ruido:

Lp	Nivel instantáneo de presión sonora	[dB] (re. 2 · 10–5 Pa)
LAeq,LT	Nivel sonoro continuo equivalente global (total)a largo plazo LAeq debido a todas las fuentes y las fuente de imagen en el punto R	[dB] (re. 2 · 10–5 Pa)
LW	Nivel de potencia sonora «in situ» de una fuente puntual (en movimiento o constante)	[dB] (re. 10–12 W)
LW,i,dir	Nivel de potencia sonora «in situ» direccional para la banda de frecuencias i	[dB] (re. 10–12 W)
LW′	Nivel medio de potencia sonora «in situ» por metro de fuente lineal	[dB/m] (re. 10–12 W)

Otros parámetros físicos:

p	Raíz cuadrática media (r.m.s.) de la presión sonora instantánea	[Pa]
p0	Presión sonora de referencia = 2 · 10–5 Pa	[Pa]
W0	Potencia sonora de referencia = 10–12 W	[vatio]

2.1.2. Marco de calidad.

Precisión de los valores de entrada.

Todos los valores de entrada que afecten al nivel de emisiones de una fuente se determinarán al menos con una precisión correspondiente a una incertidumbre de ± 2dB(A) en el nivel de emisiones de la fuente (dejando invariables todos los demás parámetros).

Uso de los valores por defecto.

Al aplicar el método, los datos de entrada reflejarán el uso real. En general, no se utilizarán valores de entrada por defecto ni estimados. Los valores de entrada por defecto y los estimados se aceptan si la recopilación de datos reales supone costes muy altos.

Calidad del software usado para los cálculos.

El software utilizado para realizar los cálculos deberá acreditar la conformidad con los métodos aquí descritos mediante una certificación de resultados derivados de los ensayos realizados.

El software utilizado para el cálculo de los niveles de ruido en el ambiente exterior deberá cumplir con los requerimientos establecidos en la norma ISO 17534 en lo referente a calidad y garantía de calidad acústica y a las recomendaciones generales para los ensayos (test) e interface de control de calidad, así como las recomendaciones para la aplicación del control de calidad en la ejecución de los métodos descritos en este anexo por el software de acuerdo con la norma ISO 17534-1.

2.2. Ruido del tráfico viario.

2.2.1. Descripción de la fuente.

Clasificación de los vehículos.

La fuente de ruido del tráfico viario se determinará mediante la combinación de la emisión de ruido de cada uno de los vehículos que forman el flujo del tráfico. Estos vehículos se agrupan en cinco categorías independientes en función de las características que posean en cuanto a la emisión de ruido:

Categoría 1: Vehículos ligeros.

Categoría 2: Vehículos pesados medianos.

Categoría 3: Vehículos pesados.

Categoría 4: Vehículos de dos ruedas.

Categoría 5: Categoría abierta.

En el caso de los vehículos de dos ruedas, se definen dos subclases independientes para los ciclomotores y las motocicletas de mayor potencia, ya que los modos de conducción son diversos y, además, suelen variar significativamente en número.

Se usarán las primeras cuatro categorías, y la quinta será opcional. Se prevé el establecimiento de otra categoría para los nuevos vehículos que puedan fabricarse en el futuro que presenten características suficientemente diferentes en términos de emisiones de ruido. Esta categoría podría englobar, por ejemplo, los vehículos eléctricos o híbridos o cualquier vehículo que se fabrique en el futuro que difiera significativamente de los de las categorías 1 a 4.

Los detalles de las diferentes clases de vehículos se facilitan en el cuadro [2.2.a].

Cuadro [2.2.a]

Clases de vehículos

Categoría	Nombre	Descripción		Categoría de vehículo en CE Homologación de tipo del vehículo completo1
1	Vehículos ligeros.	Turismos, camionetas ≤ 3,5 toneladas, todoterrenos2, vehículos polivalentes3, incluidos remolques y caravanas.		M1 y N1.
2	Vehículos pesados medianos.	Vehículos medianos, camionetas > 3,5 toneladas, autobuses, autocaravanas, entre otros, con dos ejes y dos neumáticos en el eje trasero.		M2, M3 y N2, N3.
3	Vehículos pesados.	Vehículos pesados, turismos, autobuses, con tres o más ejes.		M2 y N2 con remolque, M3 y N3.
4	Vehículos de dos ruedas.	4a	Ciclomotores de dos, tres y cuatro ruedas.	L1, L2, L6.
		4b	Motocicletas con y sin sidecar, triciclos y cuatriciclos.	L3, L4, L5, L7.
5	Categoría abierta.	Su definición se atendrá a las futuras necesidades.		N/A.

¹ Directiva 2007/46/CE del Parlamento Europeo y del Consejo de 5 de septiembre de 2007 (DO L 263 de 9.10.2007, p. 1) por la que se crea un marco para la homologación de los vehículos de motor y de los remolques, sistemas, componentes y unidades técnicas independientes destinados a dichos vehículos.

² Todoterrenos.

³ Vehículos polivalentes.

Número y situación de fuentes sonoras equivalentes.

En este método, cada vehículo (categorías 1, 2, 3, 4 y 5) se representa mediante una fuente de un solo punto que se irradia de manera uniforme en el semiespacio por encima del suelo. La primera reflexión sobre el pavimento se trata de manera implícita. Como se ilustra en la figura [2.2.a], esta fuente puntual se ubica a 0,05 m por encima del pavimento.

Figura [2.2.a]

Ubicación de la fuente puntual equivalente en vehículos ligeros (categoría 1), vehículos pesados (categorías 2 y 3) y vehículos de dos ruedas (categoría 4)

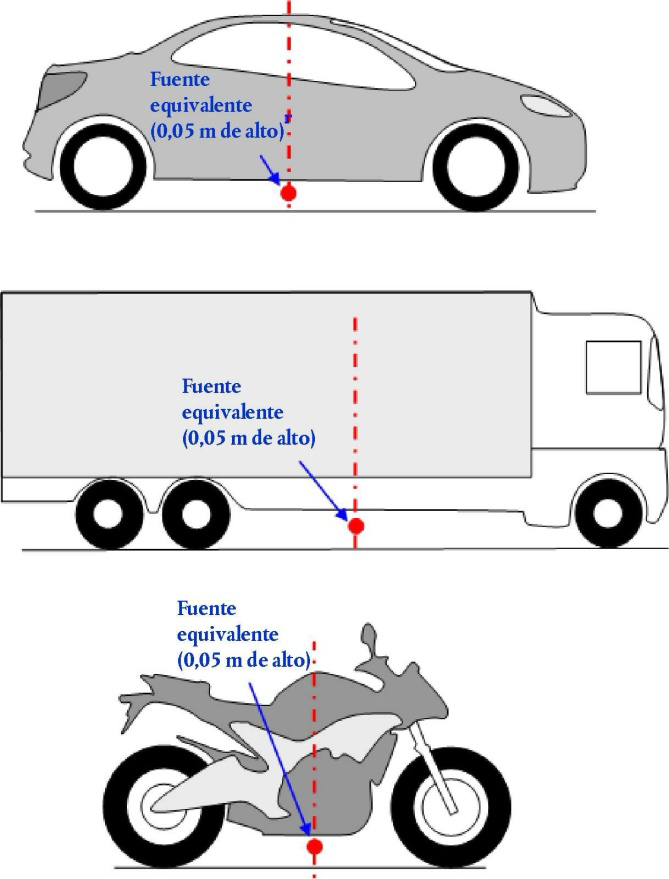
El flujo de tráfico se representa mediante una fuente lineal. Al modelizar una carretera con varios carriles, lo ideal es representar cada carril con una fuente lineal ubicada en el centro de cada carril. No obstante, también se puede dibujar una fuente lineal en el medio de una carretera de doble sentido o una fuente lineal por cada calzada en el carril exterior de carreteras con varios carriles.

Nivel de potencia sonora (Emisión).

Consideraciones generales.

La potencia sonora de la fuente se define en el «campo semilibre», por lo que la potencia sonora comprende el efecto de la reflexión sobre el suelo inmediatamente debajo de la fuente modelizada en la que no existen objetos perturbadores en su entorno más próximo, salvo en el caso de la reflexión sobre el pavimento que no se produce inmediatamente debajo de la fuente modelizada.

Intensidad de tráfico.

La emisión de un flujo de tráfico se representa mediante una fuente lineal caracterizada por su potencia sonora direccional por metro y por frecuencia. Esto se corresponde con la suma de la emisión sonora de cada uno de los vehículos del flujo de tráfico, teniendo en cuenta el tiempo durante el cual los vehículos circulan por el tramo de carretera considerado. La implementación de cada vehículo del flujo requiere la aplicación de un modelo de tráfico.

Si se supone un tráfico continuo de vehículos Q_m de la categoría m por hora, con una velocidad media de v_m (en km/h), la potencia sonora direccional por metro en la banda de frecuencias i de la fuente lineal L_Weq,line,i,m se define mediante:

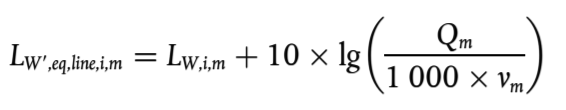
(2.2.1)

donde

L_W,i,m es el nivel de potencia sonora direccional de un único vehículo.

L_W′,m se expresa en dB (re. 10^–12 W/m). Los niveles de potencia sonora se calculan para cada banda de octava i comprendida entre 63 Hz y 8 kHz.

Los datos de intensidad de tráfico Q_m se expresarán como un promedio anual horario, por período de tiempo (día, tarde y noche), por clase de vehículo y por fuente lineal. Para todas las categorías se utilizarán los datos de entrada de intensidad de tráfico derivados del aforo de tráfico o de los modelos de tráfico.

La velocidad v_m es una velocidad representativa por categoría de vehículo: en la mayoría de los casos, es la velocidad máxima permitida más baja para el tramo de carretera y la velocidad máxima permitida para la categoría de vehículos. Si no se encuentran disponibles los datos de mediciones locales, se utilizará la velocidad máxima permitida para la categoría de vehículos.

Vehículo individual.

En la consideración de la circulación vehículos, se supone que todos los vehículos de la categoría m circulan a la misma velocidad, es decir, v_m, la velocidad media del flujo de vehículos de la categoría.

Un vehículo de carretera se modeliza mediante un conjunto de ecuaciones matemáticas que representan las principales fuentes de ruido:

1. Ruido de rodadura por la interacción producida por el contacto neumático-calzada.

2. Ruido de propulsión producido por la fuerza de transmisión (motor, escape, etc.) del vehículo. El ruido aerodinámico se incorpora a la fuente del ruido de rodadura.

En el caso de los vehículos ligeros, medianos y pesados (categorías 1, 2 y 3), la potencia sonora total se corresponde con la suma energética del ruido de rodadura y del ruido de propulsión. Por tanto, el nivel de potencia sonora total de las líneas de fuentes m = 1, 2 o 3 se define mediante:

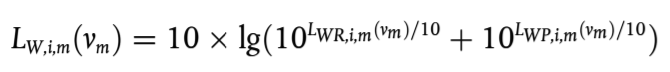
(2.2.2)

donde L_WR,i,m es el nivel de potencia sonora para el ruido de rodadura y L_WP,i,m, el nivel de potencia sonora para el ruido de propulsión. Esto es válido para todas las gamas de velocidades. Para velocidades inferiores a 20 km/h, se utilizará el mismo nivel de potencia sonora definido por la fórmula para v_m = 20 km/h.

Para los vehículos de dos ruedas (categoría 4), para la fuente solo se considera el ruido de propulsión:

L_{W,i,m = 4}(v_{m =4}) = L_{WP,i,m =4}(v_{m = 4})

(2.2.3)

Esto es válido para todos los rangos de velocidades. Para velocidades inferiores a 20 km/h, se utilizará el mismo nivel de potencia sonora definido por la fórmula para v_m = 20 km/h.

2.2.2. Condiciones de referencia.

Los coeficientes y las ecuaciones de caracterización de la fuente son válidos para las siguientes condiciones de referencia:

‒ una velocidad constante del vehículo;

‒ una carretera sin pendiente;

‒ una temperatura del aire τ_ref = 20 °C;

‒ un pavimento de referencia virtual, formado por aglomerado asfáltico denso 0/11 y pavimento mezclado SMA 0/11, con una antigüedad de entre 2 y 7 años y en un estado de mantenimiento representativo;

‒ un pavimento seco;

‒ neumáticos sin clavos.

2.2.3. Ruido de rodadura.

Ecuación general.

El nivel de potencia sonora del ruido de rodadura en la banda de frecuencias i para un vehículo de la clase m = 1, 2 o 3 se define como:

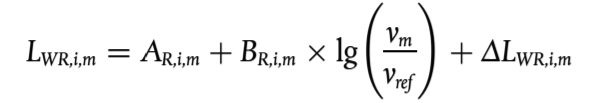
(2.2.4)

Los coeficientes A_R,i,m y B_R,i,m se dan en bandas de octava para cada categoría de vehículo y para una velocidad de referencia v_ref = 70 km/h. ΔL_WR,i,m se corresponde con la suma de los coeficientes de corrección que se han de aplicar a la emisión de ruido de rodadura para condiciones específicas del firme o del vehículo diferentes de las condiciones de referencia:

ΔL_WR,i,m = ΔL_WR,road,i,m + ΔL_{studdedtyres,i,m} + ΔL_WR,acc,i,m + ΔL_W,temp

(2.2.5)

ΔL_WR,road,i,m representa el efecto que tiene en el ruido de rodadura un pavimento con propiedades sonoras distintas a las del pavimento (superficie de rodadura de referencia virtual, como se define en el capítulo 2.2.2. Incluye tanto el efecto en la propagación como en la generación.

ΔL_{studded tyres,i,m} es un coeficiente de corrección que tiene en cuenta el ruido de rodadura mayor de los vehículos ligeros equipados con neumáticos con clavos.

ΔL_WR,acc,i,m tiene en cuenta el efecto que tiene en el ruido de rodadura en una intersección con semáforos o una glorieta. Integra el efecto que la variación de velocidad tiene en la emisión sonora.

ΔL_W,temp es un término de corrección para una temperatura media τ distinta de la temperatura de referencia τ_ref = 20 °C.

Corrección para los neumáticos con clavos.

En situaciones en que un número importante de vehículos ligeros del flujo de tráfico usan neumáticos con clavos durante varios meses al año, se tendrá en cuenta el efecto inducido en el ruido de rodadura. Para cada vehículo de la categoría m = 1 equipado con neumáticos con clavos, calcula un incremento del ruido de rodadura en función de la velocidad mediante las expresiones siguientes:

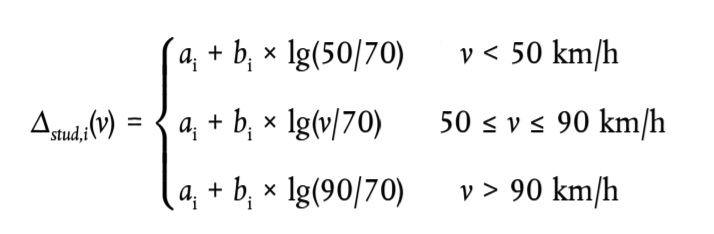
(2.2.6)

donde los coeficientes a_i y b_i se proporcionan para cada banda de octava.

El aumento de la emisión de ruido de rodadura se obtendría teniendo en cuenta únicamente la parte proporcional de vehículos ligeros con neumáticos con clavos durante un período limitado T_s (en meses) a lo largo del año. Si Q_stud,ratio es la ratio de la intensidad horaria de vehículos ligeros equipados con neumáticos con clavos que circulan en un período T_s (en meses), entonces la proporción media anual de vehículos equipados con neumáticos con clavos p_s se expresa mediante:

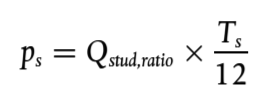
(2.2.7)

La corrección resultante que se aplicará a la emisión de potencia sonora de rodadura debido al uso de neumáticos con clavos para vehículos de la categoría m = 1 en la banda de frecuencias i será:

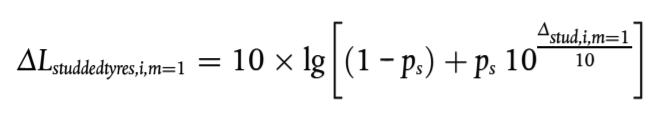
(2.2.8)

Para los vehículos de todas las demás categorías no se aplicará ninguna corrección:

ΔL_{studdedtyres,i,m ≠ 1} = 0

(2.2.9)

Efecto de la temperatura del aire en la corrección del ruido de rodadura.

La temperatura del aire afecta a la emisión de ruido de rodadura; de hecho, el nivel de potencia sonora de rodadura disminuye cuando aumenta la temperatura del aire. Este efecto se introduce en la corrección por tipo de pavimento. Las correcciones del pavimento suelen evaluarse para una temperatura del aire de τ_ref = 20 °C. Si la temperatura del aire media anual en °C es diferente, la emisión del ruido de rodadura se corregirá con la fórmula:

ΔL_W,temp,m(τ) = K_m × (τ_ref – τ)

(2.2.10)

El término de corrección es positivo (es decir, que el ruido aumenta) para temperaturas inferiores a 20 °C y negativo (es decir, que el ruido disminuye) para temperaturas más altas. El coeficiente K depende de las características del pavimento y de los neumáticos y, en general, refleja cierta dependencia de la frecuencia. Se aplicará un coeficiente genérico K_{m = 1} = 0,08 dB/°C para vehículos ligeros (categoría 1) y K_{m = 2} = K_{m = 3} = 0,04 dB/°C para vehículos pesados (categorías 2 y 3) para todos los pavimentos. El coeficiente de corrección se aplicará por igual a todas las bandas de octava desde 63 hasta 8 000 Hz.

2.2.4. Ruido de propulsión.

Ecuación general.

La emisión de ruido de propulsión comprende todas las contribuciones del motor, el tubo de escape, las marchas, caja de cambios, engranajes, la entrada de aire, etc. El nivel de potencia sonora del ruido de propulsión en la banda de frecuencias i para un vehículo de clase m se define como:

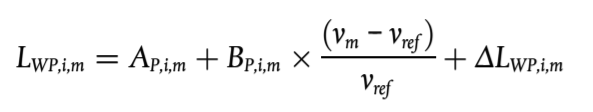
(2.2.11)

Los coeficientes A_P,i,m y B_P,i,m se dan en bandas de octava para cada categoría de vehículo y para una velocidad de referencia v_ref = 70 km/h.

ΔL_WP,i,m se corresponde con la suma de los coeficientes de corrección que se han de aplicar a la emisión de ruido de propulsión para condiciones de conducción específicas o condiciones regionales diferentes de las condiciones de referencia:

ΔL_WP,i,m = ΔL_WP,road,i,m + ΔL_WP,grad,i,m + ΔL_WP,acc,i,m

(2.2.12)

ΔL_WP,road,i,m tiene en cuenta el efecto del pavimento en el ruido de propulsión debido a la absorción. El cálculo se realizará conforme a lo especificado en el capítulo 2.2.6.

ΔL_WP,acc,i,m y ΔL_WP,grad,i,m tiene en cuenta el efecto de las pendientes de la carretera y de la aceleración y la desaceleración de los vehículos en las intersecciones. Se calcularán según lo previsto en los capítulos 2.2.4 y 2.2.5, respectivamente.

Efecto de las pendientes de la carretera.

La pendiente de la carretera tiene dos efectos en la emisión de ruido del vehículo: en primer lugar, afecta a la velocidad del vehículo y, por consiguiente, a la emisión de ruido de rodadura y de propulsión del vehículo; en segundo lugar, afecta a la carga y la velocidad del motor por la elección de la marcha y, por tanto, a la emisión de ruido de propulsión del vehículo. En esta sección solo se aborda el efecto en el ruido de propulsión, suponiendo una velocidad constante.

El efecto que la pendiente de la carretera tiene en el ruido de propulsión se tiene en cuenta mediante un término de corrección ΔL_WP,grad,m, que es una función de la pendiente s (en %), la velocidad del vehículo v_m (en km/h) y la clase de vehículo m. En el caso de una circulación en dos sentidos, es necesario dividir el flujo en dos componentes y corregir la mitad para la subida y la otra mitad para la bajada. El término de corrección se atribuye a todas las bandas de octava por igual:

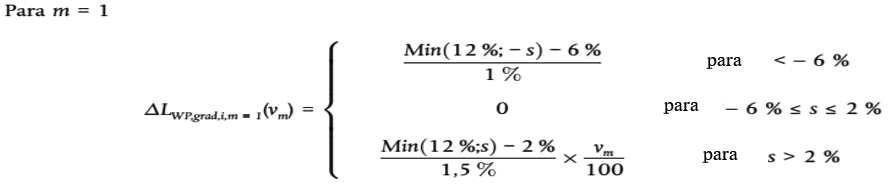
(2.2.13)

(2.2.14)

(2.2.15)

(2.2.16)

La corrección ΔL_WP,grad,m incluye de forma implícita el efecto que la pendiente tiene en la velocidad.

2.2.5. Efecto de la aceleración y desaceleración de los vehículos.

Antes y después de las intersecciones reguladas por semáforos y las glorietas, se aplicará una corrección para el efecto de la aceleración y la desaceleración, tal y como se describe a continuación.

Los términos de corrección para el ruido de rodadura, ΔL_WR,acc,m,k, y para el ruido de propulsión, ΔL_WP,acc,m,k, son funciones lineales de la distancia x (en m) desde la fuente puntual hasta la intersección más cercana de la fuente lineal correspondiente con otra fuente lineal. Estos términos se atribuyen a todas las bandas de octava por igual:

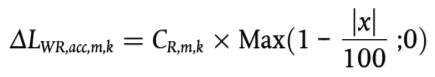
(2.2.17)

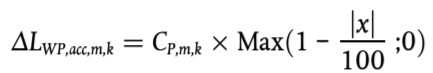
(2.2.18)

Los coeficientes C_R,m,k y C_P,m,k dependen del tipo de intersección k (k = 1 para una intersección regulada por semáforos; k = 2 para una glorieta) y se proporcionan para cada categoría de vehículos. La corrección comprende el efecto del cambio de velocidad al aproximarse a una intersección o a una glorieta o al alejarse de ella.

Tenga en cuenta que a una distancia |x| ≥ 100 m, ΔL_WR,acc,m,k = ΔL_WP,acc,m,k = 0.

2.2.6. Efecto del tipo de pavimento (superficie de rodadura).

Principios generales.

Si se trata de pavimentos con propiedades sonoras distintas a las del pavimento de referencia, se aplicará un término de corrección por bandas de frecuencia para el ruido de rodadura y el ruido de propulsión.

El término de corrección del pavimento para la emisión de ruido de rodadura se calcula mediante la expresión:

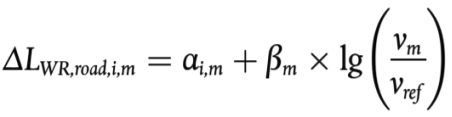
(2.2.19)

Donde:

α_i,m es la corrección en dB a la velocidad de referencia v_ref para la categoría m (1, 2 o 3) y para la banda de frecuencia i.

β_m es el efecto de la velocidad en la reducción de ruido de rodadura para la categoría m (1, 2 o 3) y es idéntico para todas las bandas de frecuencias.

El término de corrección del pavimento para la emisión de ruido de propulsión se obtiene mediante la expresión:

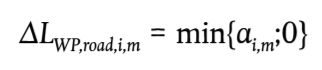
(2.2.20)

Las superficies absorbentes reducen el ruido de propulsión, mientras que las superficies no absorbentes no lo aumentan.

Efecto de la antigüedad del pavimento en el ruido de rodadura.

Las características sonoras de las superficies de rodadura varían con la antigüedad y el nivel de mantenimiento, con una tendencia a que el ruido sea mayor con el paso del tiempo. En este método, los parámetros de la superficie de rodadura se han establecido para que sean representativos del comportamiento acústico del tipo de superficie de rodadura como promedio con respecto a su vida útil representativa y suponiendo que se realiza un mantenimiento adecuado.

2.3. Ruido ferroviario.

2.3.1. Descripción de la fuente.

Clasificación de los vehículos.

Definición de vehículo y tren.

A los efectos de este método de cálculo del ruido, un vehículo se define como cualquier subunidad ferroviaria independiente de un tren (normalmente una locomotora, un automotor, coche de viajeros o un vagón de carga) que se pueda mover de manera independiente y que se pueda desacoplar del resto del tren. Se pueden dar algunas circunstancias específicas para las subunidades de un tren que forman parte de un conjunto que no se puede desacoplar, por ejemplo, compartir un bogie entre ellas. A los efectos de este método de cálculo, todas estas subunidades se agrupan en un único vehículo.

Asimismo, para este método de cálculo, un tren consta de una serie de vehículos acoplados.

En el cuadro [2.3.a] se define un lenguaje común para describir los tipos de vehículos incluidos en la base de datos de las fuentes. En él se presentan los descriptores correspondientes que se usarán para clasificar todos los vehículos. Estos descriptores se corresponden con las propiedades del vehículo, que afectan a la potencia sonora direccional por metro de línea fuente equivalente modelizada.

El número de vehículos de cada tipo se determinará en cada tramo de vía para cada período considerado en el cálculo del ruido. Se expresará como un número promedio de vehículos por hora, que se obtiene al dividir el número total de vehículos que circulan durante un período de tiempo determinado entre la duración en horas de dicho período (por ejemplo, 24 vehículos en 4 horas dan como resultado 6 vehículos por hora). Se consideran todos los tipos de vehículos que circulan por cada tramo de vía.

Cuadro [2.3.a]

Clasificación y descriptores para los vehículos ferroviarios

Dígito	1	2	3	4
Descriptor	Tipo de vehículo	Número de ejes por vehículo	Tipo de freno	Elementos reductores de Ruido en las ruedas
Explicación del descriptor	Una letra que describe el tipo	El número real de ejes	Una letra que describe el tipo de freno	Una letra que describe el tipo de medida de la reducción de ruido
Posibles descriptores	h vehículo de alta velocidad (> 200 km/h)	1	c bloque de fundición	n ninguna medida
	m coches de pasajeros autopropulsados	2	k zapatas de metal sinterizado (composite)	d amortiguadores
	p coches de pasajeros remolcados	3	n frenado sin zapatas, como disco, tambor, magnético	s pantallas
	c coche autopropulsado y no autopropulsado de tranvía o metro ligero	4		o otros
	d locomotora diésel	etc.
	e locomotora eléctrica
	a cualquier vehículo genérico para el transporte de mercancías
	o otros (como vehículos de conservación)

Clasificación de las vías y estructura portante.

Las vías existentes pueden variar porque hay varios elementos que contribuyen a las propiedades sonoras y las caracterizan. Los tipos de vías utilizados en este método se indican en el cuadro [2.3.b] siguiente. Algunos de los elementos influyen significativamente en las propiedades sonoras, mientras que otros solo tienen efectos secundarios. En general, los elementos más importantes que influyen en la emisión de ruido ferroviario son: la rugosidad del carril, la rigidez de la placa de asiento del carril, la base de la vía, las juntas de los carriles y el radio de curvatura de la vía. De forma alternativa, se pueden definir las propiedades generales de la vía y, en este caso, la rugosidad del carril y la tasa de deterioro de la vía según la norma ISO 3095 son dos parámetros esenciales desde el punto de vista acústico, además del radio de curvatura de la vía.

El tramo de vía se define como una parte de una única vía, en una línea ferroviaria o en una estación, en la que no cambian los componentes básicos ni las propiedades físicas de la vía.

En el cuadro [2.3.b] se define un lenguaje común para describir los tipos de vías incluidos en la base de datos de las fuentes.

Cuadro [2.3.b]

Dígito	1	2	3	4	5	6
Descriptor	Base de la vía	Rugosidad del carril	Tipo de placa de asiento	Medidas adicionales	Juntas de los carriles	Curvatura
Explicación del descriptor	Tipo de base de la vía	Indicadores de la rugosidad	Representa una indicación de la rigidez acústica	Una letra que describe el dispositivo acústico	Presencia de juntas y sepa- raciones	Indica el radio de curvatura en m
Códigos permitidos	B Balasto	E Buena conservación y buen funcionamiento	S Suave (150-250 MN/m)	N Ninguna	N Ninguna	N Vía recta
	S Vía en placa	M Conservación normal	M Media (250 a 800 MN/m)	D Amortiguador del carril	S Cambio o junta únicos	L Baja (1 000-500 m)
	L Puente con vía con balasto	N Mala conservación	H Rígido (800-1 000 MN/m)	B Pantalla de baja altura	D Dos juntas o cambios por 100 m	M Media (Menos de 500 m y más de 300 m)
	N Puente sin balasto	B Sin mantenimiento y en mal estado		A Placa de absorción acústica en la vía en placa	M Más de dos juntas o cambios por 100 m	H Alta (Menos de 300 m)
	T Vía embebida			E Carril embebido
	O Otro			O Otro

Número y situación de fuentes sonoras equivalentes.

Figura [2.3.a]

Situación de fuentes sonoras equivalentes

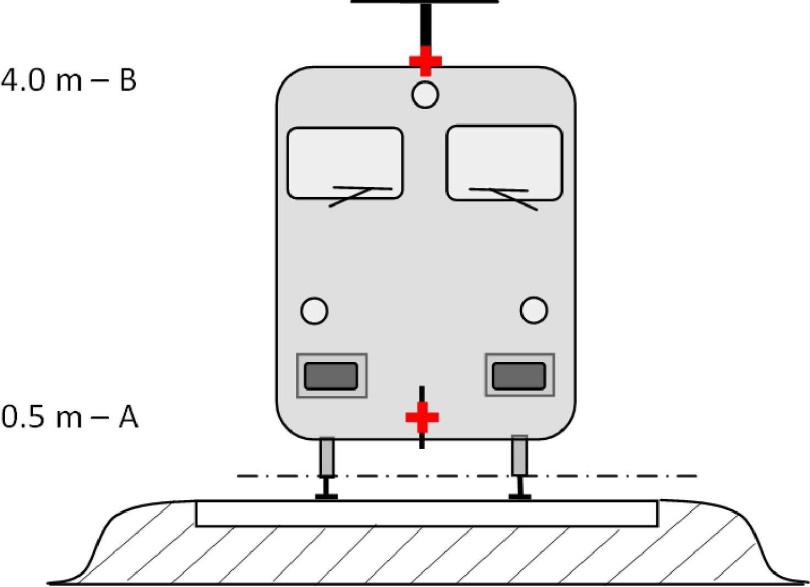
Las distintas fuentes lineales de ruido equivalentes se ubican a diferentes alturas y en el centro de la vía. Todas las alturas se refieren al plano tangencial a las dos superficies superiores de los dos carriles.

Las fuentes equivalentes comprenden diferentes fuentes físicas (índice p). Estas fuentes físicas se dividen en dos categorías distintas en función del mecanismo de generación, y son: 1) el ruido de rodadura (incluida no solo la vibración de la base del carril y la vía y la vibración de las ruedas, sino también, si procede, el ruido de la superestructura de los vehículos destinados al transporte de mercancías); 2) el ruido de tracción; 3) el ruido aerodinámico; 4) el ruido de impacto (en cruces, cambios y juntas); 5) el ruido generado por los chirridos, y 6) el ruido generado por efectos adicionales como puentes y viaductos.

1) El ruido de rodadura se origina debido a la rugosidad de las ruedas y de las cabezas de carril, a través de tres vías de transmisión a las superficies radiantes (carril, ruedas y superestructura). La fuente se ubica a h = 0,5 m (superficies radiantes A) para representar la contribución de la vía, incluidos los efectos de la superficie de las vías, en particular en las vías en placa (según la zona de propagación), para representar la contribución de la rueda y la contribución de la superestructura del vehículo en relación con el ruido (en el caso de los trenes de mercancías).

2) Las alturas de las fuentes equivalentes para la consideración del ruido de tracción varían entre 0,5 m (fuente A) y 4,0 m (fuente B), en función de la posición física del componente de que se trate. Las fuentes como las transmisiones y los motores eléctricos normalmente estarán a una altura del eje de 0,5 m (fuente A). Las rejillas de ventilación y las salidas de aire pueden estar a varias alturas; el sistema de escape del motor en los vehículos diésel suelen estar a una altura de 4,0 m (fuente B). Otras fuentes de tracción, como los ventiladores o los bloques motor diésel, pueden estar a una altura de 0,5 m (fuente A) o de 4,0 m (fuente B). Si la altura exacta de la fuente se encuentra entre las alturas del modelo, la energía sonora se distribuirá de manera proporcional sobre las alturas de fuentes adyacentes más próximas.

Por este motivo, se prevén dos alturas de fuentes mediante el método a 0,5 m (fuente A), 4,0 m (fuente B), y la potencia sonora equivalente asociada se distribuye entre las dos en función de la configuración específica de las fuentes en el tipo de unidad.

3) Los efectos del ruido aerodinámico se asocian con la fuente a 0,5 m (lo que representa las cubiertas y las pantallas, fuente A) y la fuente a 4,0 m (modelización por aparatos de techo y pantógrafos, fuente B). La opción de considerar una fuente a 4,0 m para los efectos del pantógrafo constituye un modelo muy sencillo y ha de considerarse detenidamente si el objetivo es elegir una altura apropiada de la barrera acústica.

4) El ruido de impacto se asocia con la fuente a 0,5 m (fuente A).

5) El ruido de los chirridos se asocia con las fuentes a 0,5 m (fuente A).

6) El ruido de impacto en puentes y viaductos se asocia con la fuente a 0,5 m (fuente A).

2.3.2. Nivel de potencia sonora. Emisión.

Ecuaciones generales.

Vehículo individual.

El modelo de ruido del tráfico ferroviario, de forma análoga al ruido del tráfico viario, obtiene el nivel de la potencia sonora de una combinación específica de tipo de vehículo y tipo de vía que satisface una serie de requisitos descritos en la clasificación de vehículos y vías, partiendo de un conjunto de niveles de potencia sonora para cada vehículo (L_W,0).

Intensidad de tráfico.

La emisión de ruido originado por la circulación de trenes en cada vía deberá representarse mediante un conjunto de dos fuentes lineales caracterizadas por su nivel de potencia sonora direccional por metro y por banda de frecuencias. Esto se corresponde con la suma de las emisiones de ruido de cada uno de los vehículos que circulan y, en el caso específico de los vehículos parados, se tiene en cuenta el tiempo que los vehículos pasan en el tramo ferroviario considerado.

El nivel de potencia sonora direccional por metro y por banda de frecuencias, debido a todos los vehículos que circulan por cada tramo de vía de un determinado tipo de vía (j), se define de la siguiente forma:

– para cada banda de frecuencias (i);

– para cada altura de fuente determinada (h) (para las fuentes a 0,5 m h = 1 y a 4,0 m h = 2),

Y es la suma de la energía de todas las contribuciones de todos los vehículos que circulan por el tramo de vía específico j. Estas contribuciones corresponden a:

– de todos los tipos de vehículos (t)

– a diferentes velocidades (s)

– en condiciones de circulación particulares (velocidad constante) (c)

– para cada tipo de fuente física (rodadura, impacto, chirridos, tracción, aerodinámica y fuentes con otros efectos, como por ejemplo el ruido de los puentes) (p).

Para calcular el nivel de potencia sonora direccional por metro (dato de entrada en la parte de propagación) debido al tráfico mixto en el tramo de vía j, se usa la expresión siguiente:

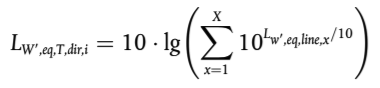
(2.3.1)

donde

T_ref = período de tiempo de referencia para el que se considera el tráfico promedio

x = número total de combinaciones existentes de i, t, s, c, p para cada tramo de la vía j

t = índice para los tipos de vehículo en el tramo de vía j

s = índice para la velocidad del tren: hay tantos índices como número de velocidades medias de circulación diferentes en el tramo de vía j

c = índice para las condiciones de circulación: 1 (para velocidad constante), 2 (ralentí)

p = índice para los tipos de fuentes físicas: 1 (para ruido de rodadura y de impacto), 2 (chirrido en las curvas), 3 (ruido de tracción), 4 (ruido aerodinámico), 5 (otros efectos)

L_{W′,eq,line,x} = nivel de potencia sonora direccional x por metro para una fuente lineal de una combinación de t, s, r, p en cada tramo de vía j

Si se supone una intensidad de circulación constante de vehículos Q por hora, con una velocidad media v, como promedio en cada momento, habrá un número equivalente de vehículos Q/v por unidad de longitud del tramo de la vía ferroviaria. La emisión de ruido debido a la circulación de trenes en términos de nivel de potencia sonora direccional por metro L_W′,eq,line (expresada en dB/m (re. 10^–12 W)) se obtiene mediante la expresión:

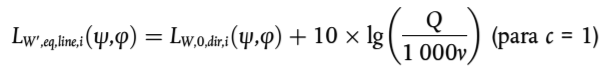
(2.3.2)

donde

– Q es el número de vehículos por hora en el tramo de vía j para el tipo de vehículo t, con una velocidad media del tren s y unas condiciones de circulación c

– v es la velocidad en el tramo de vía j para el tipo de vehículo t y con una velocidad media del tren s

– L_W,0,dir es el nivel de potencia sonora direccional del ruido específico (rodadura, impacto, chirrido, frenado, tracción, aerodinámico y otros efectos) de un único vehículo en las direcciones ψ, φ definidas con respecto a la dirección en que se mueve el vehículo (véase la figura [2.3.b]).

En el caso de una fuente estacionaria, como durante el ralentí, se supone que el vehículo permanecerá durante un tiempo total T_idle en una ubicación dentro de un tramo de vía con una longitud L. Por tanto, siendo T_ref el período de tiempo de referencia para la evaluación del ruido (por ejemplo, 12 horas, 4 horas u 8 horas), el nivel de potencia sonora direccional por unidad de longitud en el tramo de vía se define mediante:

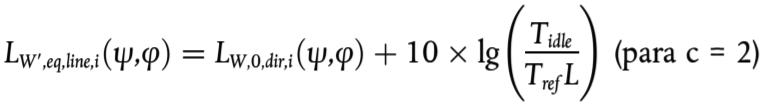
(2.3.4)

En general, el nivel de potencia sonora direccional se obtiene de cada fuente específica como:

L_{W,0,dir,i(ψ,φ)} = L_W,0,i + ΔL_W,dir,vert,i + ΔL_W,dir,hor,i

(2.3.5)

donde

– ΔL_W,dir,vert,i es la función de la corrección por directividad vertical (adimensional) de ψ (figura [2.3.b])

– ΔL_W,dir,vert,i es la función de la corrección por directividad horizontal (adimensional) de φ (figura [2.3.b]).

Y donde L_{W,0,dir,i(ψ,φ)}, después de hallarse en bandas de 1/3 de octava, deberá expresarse en bandas de octava sumando enérgicamente las potencias de cada banda de 1/3 de octava que integran la banda de octava correspondiente.

Figura [2.3.b]

Definición geométrica

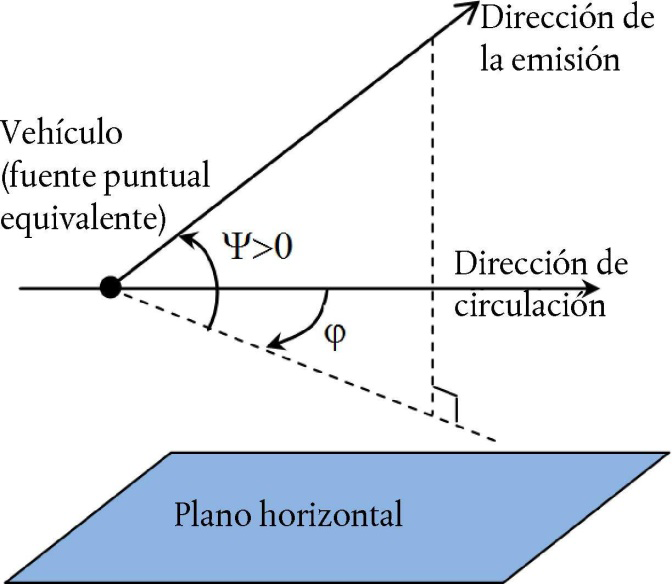
A efectos de cálculo, la potencia de la fuente se expresa de manera específica en términos de nivel de potencia sonora direccional por una longitud de 1 m de la vía L_{W′,tot,dir,i} para tener en cuenta la directividad de las fuentes en su dirección vertical y horizontal, mediante las correcciones adicionales.

Se consideran varios L_W,0,dir,i (ψ,φ) para cada combinación de vehículo-vía-velocidad-condiciones de circulación:

– para cada banda de frecuencias de octava de 1/3 (i)

– para cada tramo de vía (j)

– para cada altura de la fuente (h) (para fuentes a 0,5 m h = 1, a 4,0 m h = 2)

– directividad (d) de la fuente

Ruido de rodadura.

La contribución del vehículo y la contribución de la vía al ruido de rodadura se dividen en cuatro elementos básicos: la rugosidad de la rueda, la rugosidad del carril, la función de transferencia del vehículo a las ruedas y a la superestructura y la función de transferencia de la vía. La rugosidad de las ruedas y de los carriles representan la causa de la excitación de la vibración del punto de contacto entre el carril y la rueda, y las funciones de transferencia son dos funciones empíricas o modelizadas que representan todo el fenómeno complejo de la vibración mecánica y de la generación de ruido en las superficies de las ruedas, el carril, la traviesa y la subestructura de la vía. Esta separación refleja la evidencia física de que la rugosidad del carril puede excitar la vibración del mismo, pero también excitará la vibración de la rueda, y viceversa. El no incluir alguno de estos cuatro parámetros impediría la disociación de la clasificación de las vías y los trenes.

Rugosidad de la rueda y de la vía.

El ruido de rodadura originado por la rugosidad del carril y la rueda corresponde al rango de longitud de onda comprendido entre 5 y 500 mm.

Definición.

El nivel de rugosidad L_r se define como 10 veces el logaritmo de base 10 del cuadrado del valor cuadrático medio r² de la rugosidad de la superficie de rodadura de un carril o una rueda en la dirección del movimiento (nivel longitudinal) medida en μm con respecto a una longitud determinada del carril o al diámetro total de la rueda, dividida entre el cuadrado del valor de referencia r₀²:

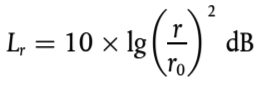
(2.3.6)

donde

r₀ = 1 μm

r = r.m.s. de la diferencia de desplazamiento vertical de la superficie de contacto con respecto al nivel medio

El nivel de rugosidad L_r suele obtenerse como una longitud de onda λ y deberá convertirse en una frecuencia f = v/λ, donde f es la frecuencia de banda central de una banda de octava determinada en Hz, λ es la longitud de onda en m y v es la velocidad del tren en m/s. El espectro de rugosidad como una función de frecuencia cambia a lo largo del eje de frecuencia para diferentes velocidades. En casos generales, tras la conversión al espectro de frecuencias en función de la velocidad, es necesario obtener nuevos valores del espectro de bandas de octava de 1/3 promediando entre dos bandas de 1/3 de octava correspondientes en el dominio de la longitud de onda. Para calcular el espectro de frecuencias de la rugosidad efectiva total correspondiente a la velocidad apropiada del tren, deberá calcularse el promedio energético y proporcional de las dos bandas de 1/3 de octava correspondientes definidas en el dominio de la longitud de onda.

El nivel de rugosidad del carril para la banda de longitud de onda i se define como L_r,TR,i

Por analogía, el nivel de rugosidad de la rueda para la banda de longitud de onda i se define como L_r,VEH,i.

El nivel de rugosidad efectiva total para la banda de longitud de onda i (L_R,tot,i) se define como la suma energética de los niveles de rugosidad del carril y de la rueda más el filtro de contacto A₃(λ) para tener en cuenta el efecto de filtrado de la banda de contacto entre el carril y la rueda, y se mide en dB:

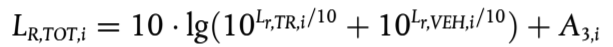
(2.3.7)

donde se expresa como una función de la banda del número de onda i correspondiente a la longitud de onda λ.

El filtro de contacto depende del tipo de carril y de rueda y de la carga.

En el método se utilizarán la rugosidad efectiva total del tramo de vía j para cada tipo de vehículo t a su velocidad v correspondiente.

Función de transferencia de vehículo, vía y superestructura.

Las funciones de transferencia independientes de la velocidad L_H,TR,i L_H,VEH,i y L_H,VEH,SUP,i se definen para cada tramo de vía j y para cada tipo de vehículo t. Relacionan el nivel de rugosidad efectiva total con la potencia sonora de la vía, las ruedas y la superestructura, respectivamente.

La contribución de la superestructura se considera solo para los vagones de mercancías, por tanto, solo para el tipo de vehículos «o».

En el caso del ruido de rodadura, las contribuciones de la vía y del vehículo se describen totalmente mediante las funciones de transferencia y mediante el nivel de rugosidad efectiva total. Cuando un tren está en ralentí, el ruido de rodadura quedará excluido.

Para la obtención del nivel de potencia sonora por vehículo, el ruido de rodadura se calcula a la altura del eje y, como dato de entrada, tiene el nivel de rugosidad efectiva total L_R,TOT,i que es una función de la velocidad del vehículo v, las funciones de transferencia de la vía, el vehículo y la superestructura L_H,TR,i, L_H,VEH,i y L_H,VEH,SUP,i, y el número total de ejes N_a:

para h = 1:

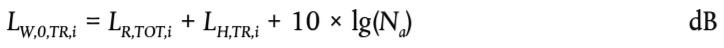
(2.3.8)

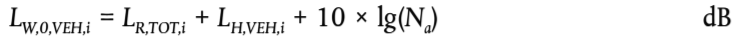
(2.3.9)

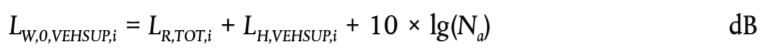
(2.3.10)

donde N_a es el número de ejes por vehículo para el tipo de vehículo t.

Figura [2.3.c]

Esquema de uso de las diferentes definiciones de rugosidad y función de transferencia

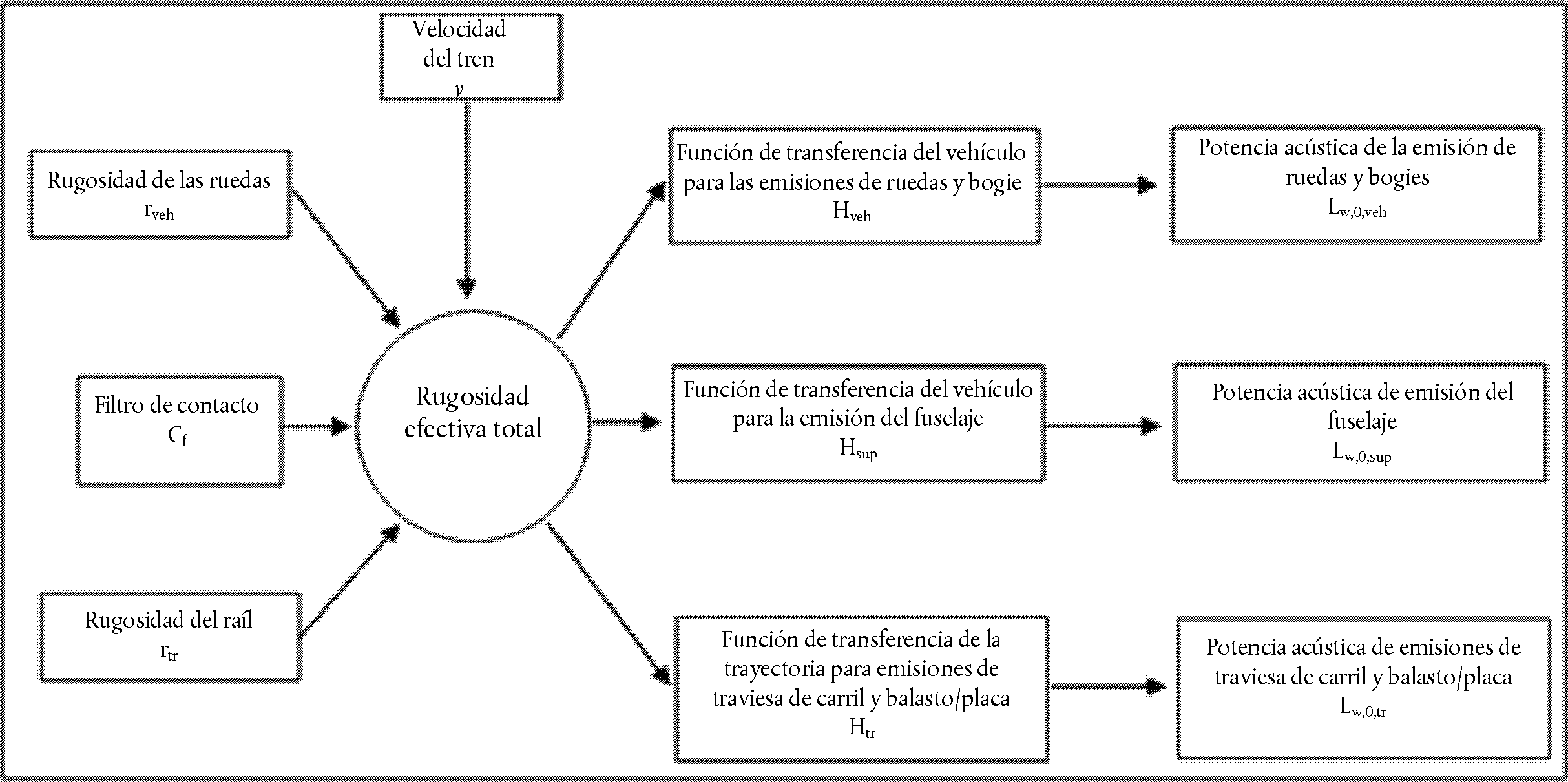
Se utilizará una velocidad mínima de 50 km/h (30 km/h para los tranvías y el metro) para determinar la rugosidad efectiva total y, por consiguiente, el nivel de potencia sonora de los vehículos (esta velocidad no afecta al cálculo de las circulaciones de vehículos) para compensar el error potencial introducido por la simplificación de la definición del ruido de rodadura, el ruido de los frenos y el ruido de impacto generado en las intersecciones y los cambios.

Ruido de impacto (cruces, cambios y juntas).

El ruido de impacto puede producirse en los cruces, los cambios y las juntas o las agujas. Puede variar en magnitud y puede ser dominante en relación con el ruido de rodadura. El ruido de impacto deberá considerarse para las vías con juntas. No se considerará el ruido de impacto generado por cambios, cruces y juntas en los tramos de vía con una velocidad inferior a 50 km/h (30 km/h para tranvías y metros), ya que la velocidad mínima de 50 km/h (30 km/h solo para tranvías y metros) se usa para incluir más efectos de acuerdo con la descripción contemplada en el capítulo del ruido de rodadura. La modelización del ruido de impacto tampoco debe considerarse en condiciones de circulación c = 2 (ralentí).

El ruido de impacto se incluye en el término del ruido de rodadura al añadir (energéticamente) un nivel de rugosidad del impacto ficticio suplementario al nivel de rugosidad efectiva total en cada tramo de vía j cuando sea pertinente. En este caso, se usará una nueva función L_{R,TOT+IMPACT,i} en lugar de L_R,TOT,i, por lo que quedará como sigue:

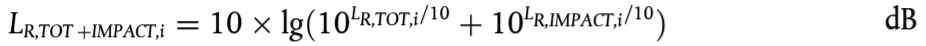
(2.3.11)

L_R,IMPACT,i es una función de la frecuencia considerada en bandas de 1/3 octava. Para obtener este espectro de frecuencias, el método incluye un espectro en función de la longitud de onda λ y deberá convertirse en frecuencias usando la relación λ = v/f, donde es la frecuencia central de la banda de 1/3 de octava en Hz y v es la velocidad s del vehículo tipo t en m/s.

El ruido de impacto dependerá de la gravedad y el número de impactos por unidad de longitud, por lo que en el caso de que se den varios impactos, el nivel de rugosidad del impacto que habrá de utilizarse en la ecuación anterior se calculará como sigue:

donde

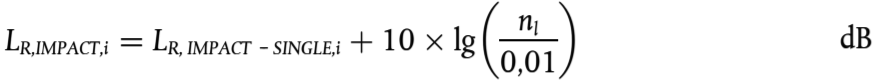
(2.3.12)

L_{R,IMPACT–SINGLE,i} es el nivel de rugosidad del impacto que se proporciona para un único impacto y n_l es el número de uniones por unidad de longitud.

El nivel de rugosidad del impacto de referencia se facilita para un número de uniones por unidad de longitud de n_l = 0,01 m^–1, que es una unión por cada 100 m de vía. Las situaciones con un número diferente s de uniones se considerarán mediante el factor de corrección n_l. Cabe señalar que, al modelizar la segmentación de la vía, deberá tenerse en cuenta el número de uniones del carril, es decir, que puede resultar necesario considerar segmentos de línea fuente separados para un tramo de vía con más uniones. La L_W,0 de la vía, la rueda y el bogie y la contribución de la superestructura se incrementan en L_R,IMPACT,i para 50 m antes y después de la unión del carril. Si se trata de una serie de uniones, el incremento se extiende a un intervalo comprendido entre – 50 m antes de la primera unión y +50 m después de la última unión.

La aplicabilidad de estos espectros de potencia sonora, por norma general, se verificará in situ.

Como valor por defecto, se utilizará n_l = 0,01.

Chirridos.

El chirrido en las curvas es una fuente especial que solo resulta relevante para las curvas y, por tanto, está localizado. Como puede ser significativo, se necesita una descripción apropiada del mismo. El chirrido en curvas suele depender de la curvatura, de las condiciones de fricción, de la velocidad del tren y de la dinámica y la geometría de las ruedas y la vía. El nivel de emisiones que se debe usar se determina para las curvas con un radio inferior o igual a 500 m y para curvas más cerradas y desvíos con un radio inferior a 300 m. La emisión de ruido debe ser específica de cada tipo de material de rodadura, ya que determinados tipos de ruedas y bogies pueden ser mucho menos propensos a los chirridos que otros.

La aplicabilidad de estos espectros de potencia sonora, por norma general, se verificará in situ, en particular en el caso de los tranvías.

Adoptando un enfoque sencillo, se considerará el ruido de los chirridos añadiendo 8 dB para R < 300 m y 5 dB para 300 m < R < 500 m al espectro de potencia sonora del ruido de rodadura para todas las frecuencias. La contribución del chirrido se aplicará a los tramos de vías ferroviarias en los que el radio se encuentre dentro de los rangos mencionados anteriormente al menos durante 50 m de longitud de la vía.

Ruido de tracción.

Aunque el ruido de tracción suele ser específico de cada condición de funcionamiento característica de velocidad constante, desaceleración, aceleración y ralentí, las únicas dos condiciones modelizadas son la velocidad constante (que es válida también cuando el tren está desacelerando o cuando está acelerando) y el ralentí. La potencia de la fuente considerada solo se corresponde con las condiciones de carga máxima, y esto implica que L_W,0,const,i = L_W,0,idling,i. Además, L_W,0,idling,i se corresponde con la contribución de todas las fuentes físicas de un vehículo determinado atribuible a una altura específica, como se describe en la sección 2.3.1.

L_W,0,idling,i se expresa como una fuente sonora estática en la posición de ralentí, para la duración del estado de ralentí, que se modeliza como una fuente puntual fija, según se describe en el siguiente capítulo dedicado al ruido industrial. Solo se considerará si los trenes están en ralentí durante más de 0,5 horas.

Estos valores pueden obtenerse o bien mediante mediciones de todas las fuentes en cada estado de funcionamiento, o bien las fuentes parciales se pueden caracterizar por separado, para determinar la dependencia que tienen de los parámetros y su fuerza relativa. Esto puede calcularse mediante la medición de un vehículo estacionario, variando las velocidades de rotación del equipo de tracción, de conformidad con la norma ISO 3095:2005. Si resulta pertinente, se tendrán que caracterizar varias fuentes sonoras de tracción, y es posible que no todas dependan de la velocidad del tren:

– El ruido del motor, como los motores diesel (incluidas las entradas de aire, el sistema de escape y el bloque motor), la transmisión, los generadores eléctricos, que dependen en gran medida de las revoluciones por minuto (rpm), y las fuentes eléctricas, como los convertidores, que pueden depender significativamente de la carga.

– El ruido de los ventiladores y de los sistemas de refrigeración, en función de las rpm del ventilador; en algunos casos, los ventiladores pueden estar directamente acoplados a la transmisión.

– Fuentes intermitentes como los compresores, las válvulas y otras con una duración característica de funcionamiento y la corrección correspondiente del ciclo de funcionamiento para la emisión de ruido.

Habida cuenta de que estas fuentes se pueden comportar de manera diferente en cada estado de funcionamiento, el ruido de la tracción se especificará según corresponda. La intensidad de una fuente se obtiene de mediciones realizadas en condiciones controladas. En general, las locomotoras tenderán a mostrar más variación en la carga en función del número de vehículos remolcados y, por consiguiente, la potencia resultante puede variar significativamente, mientras que las composiciones de trenes, como las unidades motorizadas eléctricas, las unidades motorizadas diésel y los trenes de alta velocidad, tienen una carga mejor definida.

No hay una atribución a priori de la potencia sonora de la fuente a determinadas alturas de la fuente, y esta elección dependerá del ruido específico y el vehículo evaluados. Se modelizará como una fuente A (h = 1) y una fuente B (h = 2).

Ruido aerodinámico.

El ruido aerodinámico solo se tiene en cuenta a altas velocidades por encima de 200 km/h, por lo que se debe verificar si es realmente necesario a efectos de aplicación. Si se conocen las funciones de transferencia y rugosidad del ruido de rodadura, pueden extrapolarse a velocidades más altas y se puede realizar una comparación con los datos existentes para la alta velocidad para comprobar si el ruido aerodinámico genera niveles más altos. Si las velocidades del tren en una red ferroviaria son superiores a 200 km/h, pero están limitadas a 250 km/h, en algunos casos puede no ser necesario incluir el ruido aerodinámico, dependiendo del diseño del vehículo.

La contribución del ruido aerodinámico se facilita como una función de velocidad:

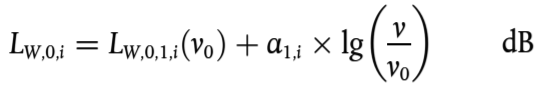 para h = 1

(2.3.13)

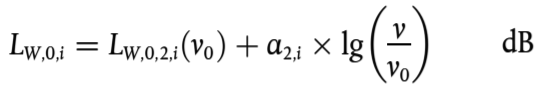 para h = 2

(2.3.14)

donde

v₀ en una velocidad en la que el ruido aerodinámico es dominante y se calcula a 300 km/h

L_W,0,1,i es un nivel de potencia sonora de referencia determinada por dos o más puntos de medida, para fuentes a alturas de fuentes conocidas, por ejemplo, el primer bogie

L_W,0,2,i es un nivel de potencia sonora de referencia determinada por dos o más puntos de medida, para fuentes a alturas de fuentes conocidas, por ejemplo, las alturas de contacto del pantógrafo

α_1,i es un coeficiente determinado por dos o más puntos de medida, para fuentes a alturas de fuentes conocidas, por ejemplo, el primer bogie

α_2,i es un coeficiente determinado por dos o más puntos de medida, para fuentes a alturas de fuentes conocidas, por ejemplo, las alturas de contacto del pantógrafo

Directividad de la fuente.

La directividad horizontal ΔL_W,dir,hor,i en dB por defecto en el plano horizontal y, por defecto, se puede asumir que se trata de un dipolo para los efectos de rodadura, impacto (juntas de carril, etc.), chirridos, frenos, ventiladores y aerodinámico, que se calcula para cada banda de frecuencias i mediante:

ΔL_W,dir,hor,i = 10 × lg (0,01 + 0,99 · sin² φ)

(2.3.15)

La directividad vertical ΔL_W,dir,ver,i en dB se calcula en el plano vertical para la fuente A (h = 1), como una función de la frecuencia central f_c,i de cada banda de frecuencias i y para – π/2 < ψ < π/2:

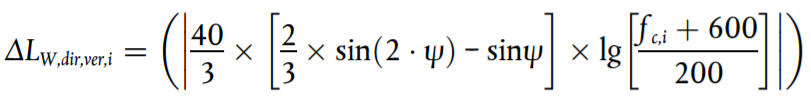
(2.3.16)

Para la fuente B (h = 2) para el efecto aerodinámico:

ΔL_W,dir,ver,i = 10 × lg(cos² ψ)  para ψ < 0

(2.3.17)

ΔL_W,dir,ver,i = 0 en todos los demás casos.

La directividad ΔL_dir,ver,i no se tiene en cuenta para la fuente B (h = 2) para los demás, ya que se supone la omnidireccionalidad para las fuentes situadas en esta posición.

2.3.3. Otros efectos.

Corrección por la radiación estructural (puentes y viaductos).

En caso de que el tramo de vía se encuentre en un puente, es necesario tener en cuenta el ruido adicional generado por la vibración del puente como resultado de la excitación ocasionada por la presencia del tren. Habida cuenta de que no es fácil modelizar la emisión de ruido del puente como una fuente adicional, a causa de las formas tan complejas de los puentes, se considera un aumento del ruido de rodadura para representar el ruido del puente. El aumento se modelizará exclusivamente incorporando un aumento fijo de la potencia sonora para cada banda de tercio de octava. Para tener en cuenta esta corrección se modifica energéticamente el nivel de potencia sonora del ruido de rodadura, y se usará el nuevo L_{W,0,rolling–and–bridge,i} en lugar de L_{W,0,rolling‒only,i}:

L_{W,0,rolling–and–bridge,}i = L_{W,0,rolling–only,i} + C_bridge  dB

(2.3.18)

donde C_bridge es una constante que depende del tipo de puente, y L_{W,0,rolling–only,i} es el nivel de potencia sonora de rodadura en el puente de que se trate que depende solo de las propiedades del vehículo y de la vía.

Corrección para otras fuentes sonoras ferroviarias.

Pueden existir otras fuentes, como los depósitos, las zonas de carga y descarga, las estaciones, las campanas, la megafonía de la estación, etc., y que se asocian con el ruido ferroviario. Estas fuentes se tratarán como fuentes sonoras industriales (fuentes sonoras fijas) y se modelizarán, si procede, según lo expuesto en el siguiente capítulo dedicado al ruido industrial.

2.4. Ruido industrial.

2.4.1. Descripción de la fuente.

Clasificación de los tipos de fuente (punto, línea y área).

Las fuentes industriales presentan dimensiones muy variables. Puede tratarse de plantas industriales grandes, así como de fuentes concentradas pequeñas, como herramientas pequeñas o máquinas operativas utilizadas en fábricas. Por tanto, es necesario usar una técnica de modelización apropiada para la fuente específica objeto de evaluación. En función de las dimensiones y de la forma en que varias fuentes independientes se extienden por una zona, todas ellas pertenecientes al mismo emplazamiento industrial, se pueden modelizar como fuentes puntuales, fuentes lineales u otras fuentes del tipo área. En la práctica, los cálculos del efecto acústico siempre se basan en las fuentes sonoras puntuales, pero se pueden usar varias fuentes sonoras puntuales para representar una fuente compleja real, que se extiende principalmente por una línea o un área.

Número y situación de fuentes sonoras equivalentes.

Las fuentes sonoras reales se modelizan mediante fuentes sonoras equivalentes representadas por una o varias fuentes puntuales, de forma que la potencia sonora total de la fuente real se corresponda con la suma de las potencias sonoras individuales atribuidas a las diferentes fuentes puntuales.

Las normas generales que deben aplicarse en la definición del número de fuentes puntuales que se usarán son:

– Las fuentes lineales o de tipo área en las que la dimensión mayor es inferior a 1/2 de la distancia entre la fuente y el receptor pueden modelizarse como fuentes puntuales exclusivas.

– Las fuentes en las que la dimensión más grande es mayor que 1/2 de la distancia entre la fuente y el receptor deben modelizarse como una serie de fuentes puntuales en una línea o como una serie de fuentes puntuales incoherentes en un área, de forma que para cada una de estas fuentes se cumpla la condición de distancia estable. La distribución por un área puede incluir la distribución vertical de las fuentes puntuales.

– Si se trata de fuentes en las que las dimensiones más grandes en términos de altura superen los 2 m o si están cerca del suelo, cabe prestar especial atención a la altura de la fuente. Duplicar el número de fuentes, redistribuyéndolas únicamente en la componente z no puede ofrecer un resultado significativamente mejor para esta fuente.

– Para todas las fuentes, duplicar el número de fuentes sobre el área de la fuente (en todas las dimensiones) no puede ofrecer un resultado significativamente mejor.

No se puede fijar de antemano la posición de las fuentes sonoras equivalentes, debido al gran número de configuraciones que un emplazamiento industrial puede tener. Por lo general, se aplicarán buenas prácticas.

Nivel de potencia sonora. Emisión.

Consideraciones generales.

La información siguiente constituye el conjunto completo de datos de entrada necesarios para los cálculos de la propagación sonora con los métodos que se utilizarán para la cartografía de ruido:

– Espectro del nivel de potencia sonora emitida en bandas de octava

– Horas de funcionamiento (día, tarde, noche o como promedio anual)

– Ubicación (coordenadas x, y) y elevación (z) de la fuente de ruido

– Tipo de fuente (punto, línea y área)

– Dimensiones y orientación

– Condiciones de funcionamiento de la fuente

– Directividad de la fuente.

Es necesario definir el nivel de potencia sonora de la fuente puntual, lineal o de área como:

– Para una fuente puntual el nivel de potencia sonora L_W y la directividad como una función de tres coordenadas ortogonales (x, y, z);

– Se pueden definir dos tipos de fuentes lineales:

– Para fuentes lineales que representan cintas transportadoras, oleoductos, etc., el nivel de potencia sonora por longitud en metros L_W′ y directividad como una función de dos coordenadas ortogonales en el eje de la línea de la fuente;

– Para fuentes lineales que representan a los vehículos en movimiento, cada uno de ellos asociado al nivel de potencia sonora L_W y directividad como una función de las dos coordenadas ortogonales en el eje de la fuente lineal y nivel de potencia sonora por metro L_W′ considerando la velocidad y el número de vehículos que circulan por esta línea durante el día, la tarde y la noche. La corrección para las horas de funcionamiento, que se añadirá al nivel de potencia sonora de la fuente para definir el nivel de potencia sonora corregido que se usará para los cálculos en cada periodo de tiempo C_W en dB, se calcula como sigue:

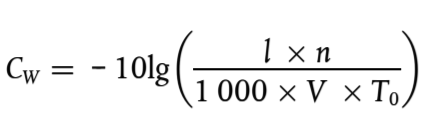
(2.4.1)

Donde:

V Velocidad del vehículo [km/h];

N Número de circulaciones de vehículos por cada período [–];

l Longitud total de la fuente [m];

– Para una fuente del tipo área, el nivel de potencia sonora por metro cuadrado L_W/m2, y sin directividad (puede ser horizontal o vertical).

Las horas de funcionamiento son una información fundamental para el cálculo de los niveles de ruido. Las horas de funcionamiento se deben facilitar para el día, la tarde y la noche y, si la propagación usa diferentes clases meteorológicas definidas durante el día, la noche y la tarde, entonces deberá facilitarse una distribución más definida de las horas de funcionamiento en subperíodos que coincidan con la distribución de las clases meteorológicas. Esta información se basará en un promedio anual.

La corrección de las horas de funcionamiento, que se añadirá al nivel de potencia sonora de la fuente para definir el nivel de potencia sonora corregida que se deberá utilizar para los cálculos en relación con cada período de tiempo C_W en dB, se calcula como sigue:

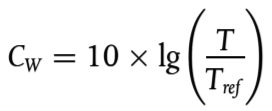
(2.4.2)

donde

T es el tiempo que la fuente está activa por cada período con carácter anual, medido en horas;

T_ref es el período de tiempo de referencia en horas (por ejemplo, para el día es 12 horas, para la tarde, 4 horas y, para la noche, 8 horas).

Para las fuentes más dominantes, la corrección de las horas de funcionamiento promedio anual se calculará al menos en una tolerancia de 0,5 dB a fin de conseguir una precisión aceptable (es equivalente a una incertidumbre inferior al 10 % en la definición del período durante el cual la fuente permanece activa).

Directividad de la fuente.

La directividad de la fuente está estrechamente relacionada con la posición de la fuente sonora equivalente próxima a las superficies cercanas. Habida cuenta de que el método de propagación tiene en cuenta la superficie cercana y la absorción sonora, es necesario tener en cuenta detenidamente la ubicación de las superficies cercanas. En general, se establecerá una distinción entre estos dos casos:

– Se considera un nivel de potencia sonora y una directividad obtenidos a partir de una situación real de una determinada fuente cuando esta se encuentra al aire libre (excluido el efecto del terreno). Esto está en consonancia con las definiciones establecidas para la propagación, siempre que se suponga que no hay ninguna superficie cercana a menos de 0,01 m de la fuente y si se incluyen las superficies a 0,01 m o más en el cálculo de la propagación;

– Se considera un nivel de potencia sonora y una directividad obtenidos a partir de una situación real de una determinada fuente cuando esta se sitúa en una ubicación específica y, por tanto, el nivel de potencia sonora de la fuente y la directividad son «equivalentes a los de la fuente real», ya que incluye la modelización del efecto de las superficies cercanas. Se define en el «campo semilibre», en función de las definiciones establecidas para la propagación. En este caso, las superficies cercanas modelizadas deberán excluirse del cálculo de la propagación.

La directividad se expresará en el cálculo como un factor ΔL_W,dir,xyz (x, y, z) que se añadirá al nivel de potencia sonora para obtener el nivel de potencia sonora direccional correcto de la fuente sonora de referencia observada desde la dirección correspondiente. El factor puede calcularse como una función del vector de dirección definido mediante (x,y,z) con

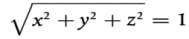
Esta directividad también puede expresarse mediante otros sistemas de coordenadas, como los sistemas de coordenadas angulares.

2.5. Cálculo de la propagación del ruido para fuentes viarias, ferroviarias e industriales.

2.5.1. Alcance y aplicabilidad del método.

En el presente documento se especifica un método para calcular la atenuación del ruido durante su propagación en exteriores. Conociendo las características de la fuente, este método predice el nivel de presión sonora continuo equivalente en un punto receptor correspondiente a dos tipos particulares de condiciones atmosféricas:

– condiciones de propagación por refracción descendente (gradiente vertical positivo de la velocidad sonora efectiva) desde la fuente al receptor;

– condiciones atmosféricas homogéneas (gradiente vertical nulo de velocidad sonora efectiva) con respecto al área completa de propagación.

El método de cálculo descrito en este documento se aplica a las infraestructuras industriales y a las infraestructuras de transporte terrestre. Por tanto, se aplica en particular a las infraestructuras viarias y ferroviarias. El transporte aéreo se incluye en el ámbito de aplicación del método de propagación solo en el caso del ruido generado durante las operaciones en tierra y excluye el despegue y el aterrizaje.

Las infraestructuras industriales que emiten ruidos tonales fuertes o impulsivos, según se describe en la norma ISO 1996-2:2007, no recaen dentro del ámbito de aplicación de este método.

El método de cálculo no facilita resultados para condiciones de propagación por refracción ascendente (gradiente vertical negativa de velocidad sonora efectiva), por lo que, para estas condiciones se utilizan las condiciones homogéneas al calcular L_den.

Para calcular la atenuación debida a la absorción atmosférica en el caso de infraestructuras de transportes, las condiciones de temperatura y humedad se aplica la norma ISO 9613-1:1996.

El método ofrece resultados por banda de octava, desde 63 Hz hasta 8 000 Hz. Los cálculos se realizan para cada una de las frecuencias centrales.

Las cubiertas parciales y los obstáculos inclinados con más de 15° de inclinación en relación con la vertical están fuera del ámbito de aplicación de este método de cálculo.

Una pantalla individual se calcula como único cálculo de difracción individual, dos o más pantallas en el mismo camino de propagación se tratan como un conjunto posterior de difracciones individuales mediante la aplicación del procedimiento descrito más adelante.

2.5.2. Definiciones utilizadas.

Todas las distancias, alturas, dimensiones y alturas utilizadas en este documento se expresan en metros (m).

La notación MN representa la distancia en 3 dimensiones (3D) entre los puntos M y N, medida con una línea recta que une estos puntos.

La notación representa la longitud de la trayectoria curva entre los puntos M y N, en condiciones favorables.

Es habitual medir las alturas reales en vertical en una dirección perpendicular al plano horizontal. Las alturas de los puntos por encima del terreno local se representan con la h, mientras que las alturas absolutas de los puntos y la altura absoluta del terreno se han de representar con la letra H.

Para tener en cuenta la orografía real del terreno a lo largo de la trayectoria de propagación, se introduce la noción de «altura equivalente», que se representa con la letra z. Esto sustituye las alturas reales en las ecuaciones del efecto de suelo.

Los niveles de presión sonora, representados por la letra mayúscula L, se expresan en decibelios (dB) por banda de frecuencias cuando se omite el índice A. A los niveles de presión sonora en decibelios dB(A) se les asigna el índice A.

La suma de los niveles de presión sonora de fuentes mutuamente incoherentes se representa mediante el signo en virtud de la siguiente definición:

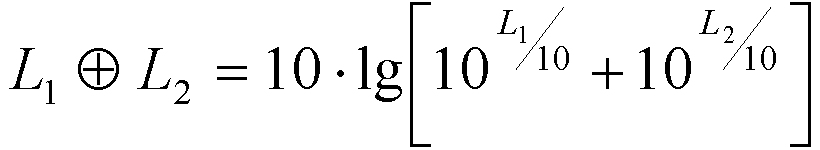
(2.5.1)

2.5.3. Consideraciones geométricas.

Segmentación de la fuente.

Las fuentes reales se describen mediante un conjunto de fuentes puntuales o, en el caso del tráfico ferroviario o del tráfico viario, mediante fuentes lineales incoherentes. El método de propagación supone que las fuentes lineales o las fuentes del tipo área se han dividido previamente para representarse mediante una serie de fuentes puntuales equivalentes. Pueden obtenerse mediante un procesamiento previo de los datos de la fuente, o bien pueden generarse informáticamente mediante un buscador de trayectorias de propagación de un software de cálculo. Los métodos de obtención están fuera del ámbito de aplicación de la metodología actual.

Trayectorias de propagación.

El método funciona en un modelo geométrico compuesto por un conjunto de superficies de obstáculos y de suelo conectadas. Una trayectoria de propagación vertical se despliega sobre uno o varios planos verticales con respecto al plano horizontal. Para trayectorias que incluyen reflexiones sobre las superficies verticales no ortogonales en el plano incidente, se considera posteriormente otro plano vertical que incluye el tramo reflejado de la trayectoria de propagación. En estos casos, cuando se usan más planos verticales para describir la trayectoria completa desde la fuente hasta el receptor, se nivelan los planos verticales, como una pantalla china desplegable.

Alturas significativas por encima del suelo.

Las alturas equivalentes se obtienen en el plano medio del suelo entre la fuente y el receptor. Se sustituye el plano real por un plano ficticio que representa el perfil medio del terreno.

Figura 2.5.a

Alturas equivalentes en relación con el suelo

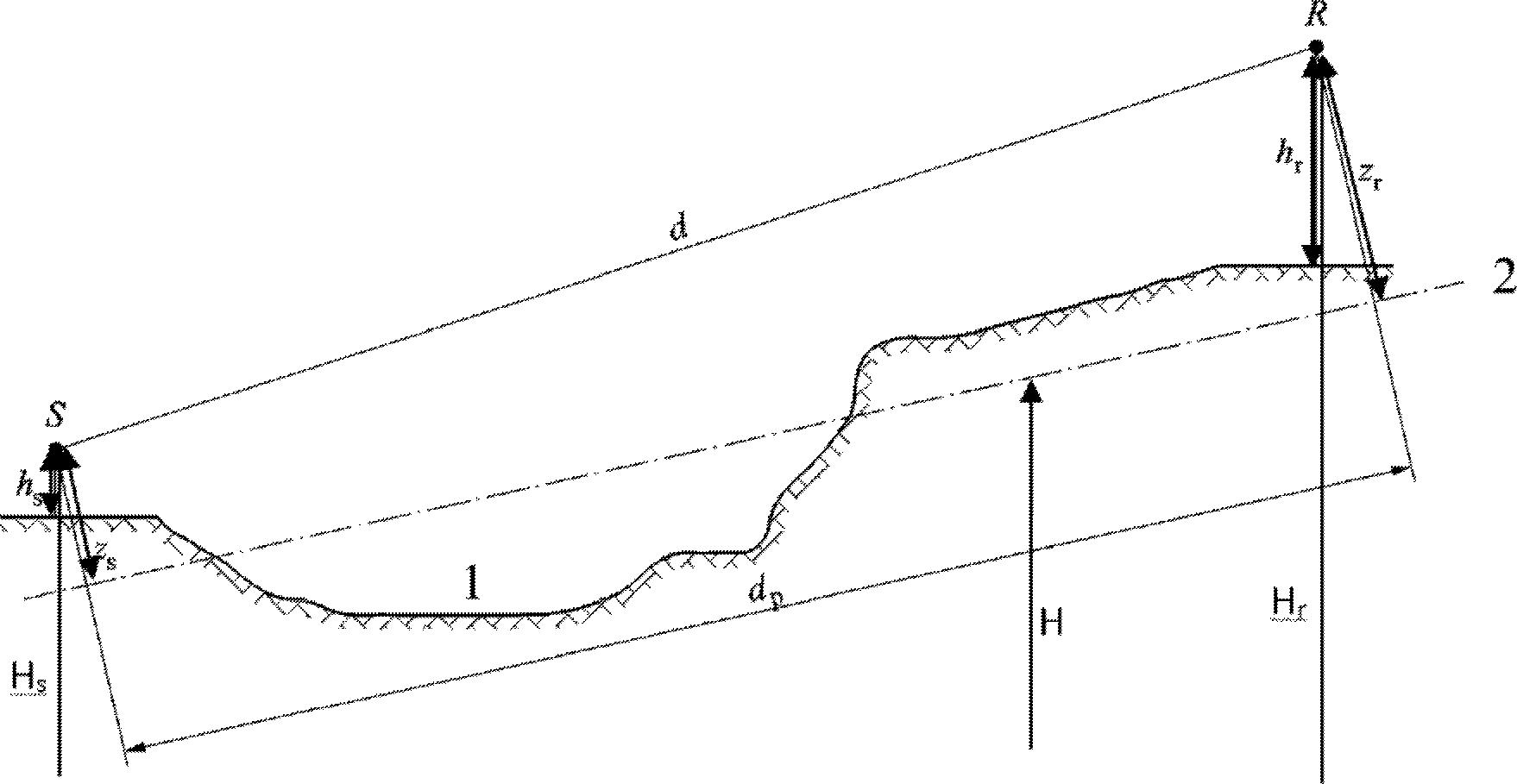
1: Orografía real

2: Plano medio

La altura equivalente de un punto es su altura ortogonal en relación con el plano medio del suelo. Por tanto, pueden definirse la altura de la fuente equivalente z_s y la altura del receptor equivalente z_r. La distancia entre la fuente y el receptor en proyección sobre el plano medio del suelo se representa con d_p.

Si la altura equivalente de un punto resulta negativa, es decir, si el punto está ubicado por debajo del plano medio del suelo, se mantiene una altura nula, y el punto equivalente es idéntico a su posible imagen.

Cálculo del plano medio.

En el plano de la trayectoria de propagación, la topografía (incluidos el terreno, los montículos, los terraplenes y otros obstáculos artificiales, los edificios, etc.) puede describirse mediante un conjunto ordenado de puntos discretos (x_k, H_k); k є {1,…, n}. Este conjunto de puntos define una polilínea, o de manera equivalente, una secuencia de segmentos rectos H_k = a_kx + b_k, x є [x_k, x_{k + 1}]; k є {1,…, n}, donde:

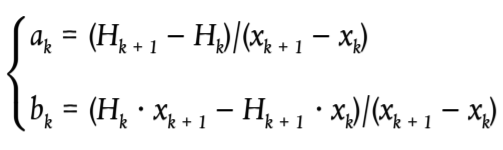
(2.5.2)

El plano medio se representa mediante la línea recta Z = ax + b; x є [x₁, x_n], que se ajusta a la polilínea mediante una aproximación mínima cuadrática. La ecuación de la línea media puede calcularse de forma analítica.

Para ello, se utiliza:

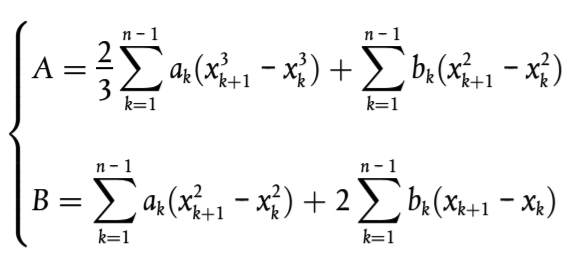
(2.5.3)

Los coeficientes de la línea recta se obtienen mediante:

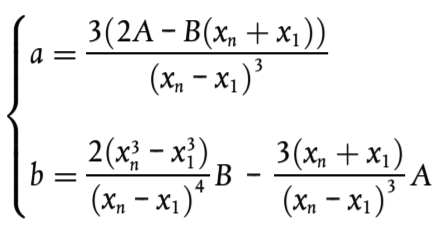
(2.5.4)

Donde los segmentos con x_{k + 1} = x_k deben ignorarse al evaluar la ecuación 2.5.3.

Reflexiones por fachadas de edificios y otros obstáculos verticales.

Las contribuciones de las reflexiones se tienen en cuenta mediante la introducción de fuentes de imágenes tal y como se describe más adelante.

2.5.4. Modelo de propagación sonora.

Para un receptor R, los cálculos se realizan siguiendo estos pasos:

1) para cada trayectoria de propagación:

– cálculo de la atenuación en condiciones favorables;

– cálculo de la atenuación en condiciones homogéneas;

– cálculo del nivel de presión sonora a largo plazo para cada trayectoria de propagación;

2) acumulación de los niveles de presión sonora a largo plazo para todas las trayectorias de propagación que afectan a un receptor determinado, de manera que se permita el cálculo del nivel de ruido total en el punto receptor.

Cabe destacar que solo las atenuaciones debidas al efecto suelo (A_ground) y a la difracción (A_dif) se ven afectadas por las condiciones meteorológicas.

2.5.5. Proceso de cálculo.

Para una fuente puntual S de nivel de potencia sonora direccional L_W,0,dir y para una banda de frecuencias determinada, el nivel de presión sonora continua equivalente en el punto receptor R en condiciones atmosféricas concretas se obtiene con las siguientes ecuaciones.

Nivel de presión sonora continua equivalente en condiciones favorables (LF) para una trayectoria de propagación (S,R).

L_F = L_W,0,dir – A_F

(2.5.5)

El término A_F representa la atenuación total a lo largo de la trayectoria de propagación en condiciones favorables, y se desglosa como sigue:

A_F = A_div + A_atm + A_boundary,F

(2.5.6)

donde

A_div es la atenuación por divergencia geométrica;

A_atm es la atenuación por absorción atmosférica;

A_boundary,F es la atenuación por el límite del medio de propagación en condiciones favorables. Puede contener los siguientes términos:

A_ground,F que es la atenuación por el terreno en condiciones favorables;

A_dif,F que es la atenuación por la difracción en condiciones favorables.

Para una trayectoria de propagación y una banda de frecuencias determinados, se pueden dar los dos escenarios siguientes:

– A_ground,F se calcula sin difracción (A_dif,F = 0 dB) y A_boundary,F = A_ground,F;

– o bien se calcula A_dif,F. El efecto suelo se tiene en cuenta en la propia ecuación A_dif,F (A_ground,F = 0 dB). De ahí se obtiene: A_boundary,F = A_dif,F.

Nivel de presión sonora continuo equivalente en condiciones homogéneas (L_H) para una trayectoria de propagación (S,R).

El procedimiento es exactamente igual al caso de las condiciones favorables descrito en la sección anterior.

L_H = L_W,0,dir – A_H

(2.5.7)

El término A_H representa la atenuación total a lo largo de la trayectoria de propagación en condiciones homogéneas, y se desglosa como sigue:

A_H = A_div + A_atm + A_boundary,H

(2.5.8)

Donde:

A_div es la atenuación por divergencia geométrica;

A_atm es la atenuación por absorción atmosférica;

A_boundary,F es la atenuación por el límite del medio de propagación en condiciones homogéneas. Puede contener los siguientes términos:

Α_ground,H que es la atenuación por el terreno en condiciones homogéneas;

A_dif,H que es la atenuación por la difracción en condiciones homogéneas.

Para una trayectoria de propagación y una banda de frecuencias determinados, se pueden dar los dos escenarios siguientes:

– A_ground,H (A_dif,H = 0 dB) se calcula sin difracción y A_boundary,H = Α_ground,H;

– o se calcula A_dif,H (Α_ground,H = 0 dB). El efecto suelo se tiene en cuenta en la propia ecuación A_dif,H. De ahí se obtiene A_boundary,H = A_dif,H.

Enfoque estadístico en zonas urbanas para un trayecto (S,R).

Dentro de las zonas urbanas, también se puede adoptar un enfoque estadístico en el cálculo de la propagación sonora por detrás de la primera línea de edificios, siempre que el método utilizado esté debidamente documentado, con información pertinente acerca de la calidad del método. Este método puede sustituir el cálculo de A_boundary,H y A_boundary,F mediante una aproximación de la atenuación total para la trayectoria directa y todas las reflexiones. El cálculo se basará en la densidad media de edificación y en la altura media de todos los edificios de la zona.

Nivel de presión sonora continuo equivalente a largo plazo para una trayectoria de propagación (S,R).

El nivel de presión sonora continuo equivalente a «largo plazo» a lo largo una trayectoria de propagación que parte de una fuente puntual determinada se obtiene de la suma logarítmica de la energía sonora ponderada en condiciones homogéneas y de la energía sonora en condiciones favorables.

Estos nivel de presión sonora continuo equivalente se ponderan con la ocurrencia media p de condiciones favorables en la dirección de la trayectoria de propagación (S,R):

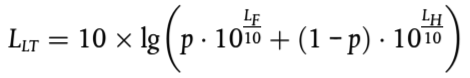
(2.5.9)

NB: Los valores de ocurrencia p se expresan en tanto por uno. Por tanto, como ejemplo, si el valor de ocurrencia es 82 %, la ecuación (2.5.9) sería p = 0,82.

Nivel de presión sonora continuo equivalente a largo plazo en el punto R para todas las trayectorias de propagación.

El nivel de presión sonora continuo equivalente total a largo plazo en el receptor para una banda de frecuencias se obtiene sumando energéticamente las contribuciones de todas las trayectorias de propagación N, incluidos todos los tipos:

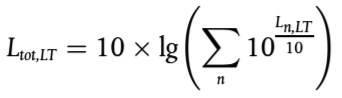
(2.5.10)

donde

n es el índice de las trayectorias de propagación entre S y R.

La consideración de las reflexiones mediante fuentes de imagen se describe más adelante. El porcentaje de ocurrencias de condiciones favorables en el caso de un trayecto reflejado en un obstáculo vertical se considera idéntico a la ocurrencia de la trayectoria de propagación directa.

Si S′ es la fuente de imagen de S, entonces la ocurrencia p′ de la trayectoria de propagación (S′,R) se considera igual a la ocurrencia p de la trayectoria de propagación (S_i,R).

Nivel de presión sonora continuo equivalente a largo plazo en el punto R en decibelios A (dBA).

El nivel de presión sonora continuo equivalente total en decibelios A (dBA) se obtiene mediante la suma de los niveles en cada banda de frecuencias:

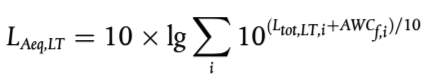
(2.5.11)

donde i es el índice de la banda de frecuencias. AWC es la corrección con ponderación A de conformidad con la norma internacional CEI 61672-1:2003.

Este nivel L_Aeq,LT constituye el resultado final, es decir, el nivel de presión sonora continuo equivalente con ponderación A a largo plazo en el punto del receptor en un intervalo de tiempo de referencia específico (por ejemplo, el día o la tarde, o la noche o un intervalo más corto durante el día, la tarde o la noche).

2.5.6. Cálculo de la propagación del ruido para fuentes viarias, ferroviarias e industriales.

Divergencia geométrica.

La atenuación por divergencia geométrica, A_div, se corresponde con una reducción del nivel de presión sonora continuo equivalente debido a la distancia de propagación. Si se trata de una fuente sonora puntual en campo libre, la atenuación en dB se obtiene mediante:

A_div = 20 × lg(d) + 11

(2.5.12)

donde d es la distancia oblicua directa en 3D entre la fuente y el receptor.

Absorción atmosférica.

La atenuación por absorción atmosférica A_atm durante la propagación por una distancia d se obtiene en dB mediante la ecuación:

A_atm = α_atm · d/1 000

(2.5.13)

donde

d es la distancia oblicua directa en 3D entre la fuente y el receptor en m;

α_atm es el coeficiente de atenuación atmosférica en dB/km a la frecuencia central nominal para cada banda de frecuencias, en virtud de la norma ISO 9613-1.

Los valores del coeficiente α_atm se proporcionan para una temperatura de 15 °C, una humedad relativa del 70 % y una presión atmosférica de 101 325 Pa. Se calculan con las frecuencias centrales exactas de la banda de frecuencias. Estos valores cumplen con la norma ISO 9613-1. Se debe usar la media meteorológica a largo plazo en caso de que la información meteorológica se encuentre disponible.

Efecto suelo.

La atenuación por el efecto suelo principalmente es el resultado de la interferencia entre el sonido reflejado y el sonido propagado directamente desde la fuente al receptor. Está físicamente vinculada a la absorción sonora del suelo sobre el cual se propaga la onda sonora. No obstante, también depende significativamente de las condiciones atmosféricas durante la propagación, ya que la curvatura de los rayos modifica la altura de la trayectoria por encima del suelo y hace que los efectos suelo y el terreno ubicado cerca de la fuente resulten más o menos importantes.

En el caso de que la propagación entre la fuente y el receptor se vea afectada por algún obstáculo en el plano de propagación, el efecto suelo se calcula por separado con respecto a la fuente y el receptor. En este caso, z_s y z_r hacen referencia a la posición de la fuente equivalente o del receptor, como se indica más adelante cuando se explica el cálculo de la difracción A_dif.

Caracterización acústica del suelo.

Las propiedades de la absorción sonora del suelo están estrechamente relacionadas con su porosidad. El suelo compacto suele ser reflectante, mientras que el suelo poroso es absorbente.

A efectos de los requisitos de cálculo operativo, la absorción sonora de un suelo se representa mediante un coeficiente adimensional G, entre 0 y 1. G es independiente de la frecuencia. En el cuadro 2.5.a se ofrecen los valores de G del suelo en exteriores. En general, la media del coeficiente G con respecto a un trayecto adopta valores comprendidos entre 0 y 1.

Cuadro 2.5.a

Valores de G para diferentes tipos de suelo

Descripción	Tipo	(kPa · s/m2)	Valor G
Muy blando (nieve o con hierba)	A	12,5	1
Suelo forestal blando (con brezo corto y denso o musgo denso)	B	31,5	1
Suelo blando no compacto (césped, hierba o suelo mullido)	C	80	1
Suelo no compacto normal (suelo forestal y suelo de pastoreo)	D	200	1
Terreno compactado y grava (césped compactado y zonas de parques)	E	500	0,7
Suelo denso compactado (carretera de grava o aparcamientos)	F	2 000	0,3
Superficies duras (hormigón y asfaltado convencional)	G	20 000	0
Superficies muy duras y densas (asfalto denso, hormigón y agua)	H	200 000	0

G_path se define como la fracción de terreno absorbente presente sobre toda la trayectoria de propagación cubierta.

Cuando la fuente y el receptor están cerca de modo que d_p≤ 30 (z_s + z_r), la distinción entre el tipo de terreno ubicado cerca de la fuente y el tipo de terreno ubicado cerca del receptor es insignificante. Para tener en cuenta este comentario, el factor de suelo G_path se corrige en última instancia como sigue:

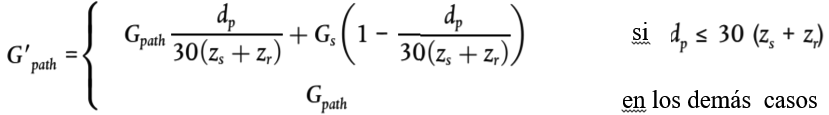
(2.5.14)

donde G_s es el factor de suelo de la fuente del tipo área. G_s = 0 para plataformas de carretera⁴ y vías en placa. G_s = 1 para vías férreas sobre balasto. No hay una regla general para el caso de las plantas y las fuentes industriales.

4 La absorción de los pavimentos de carreteras porosos se tiene en cuenta en el modelo de emisiones

G puede estar vinculada a la resistividad al flujo.

Figura 2.5.b

Determinación del coeficiente del suelo G_path sobre una trayectoria de propagación

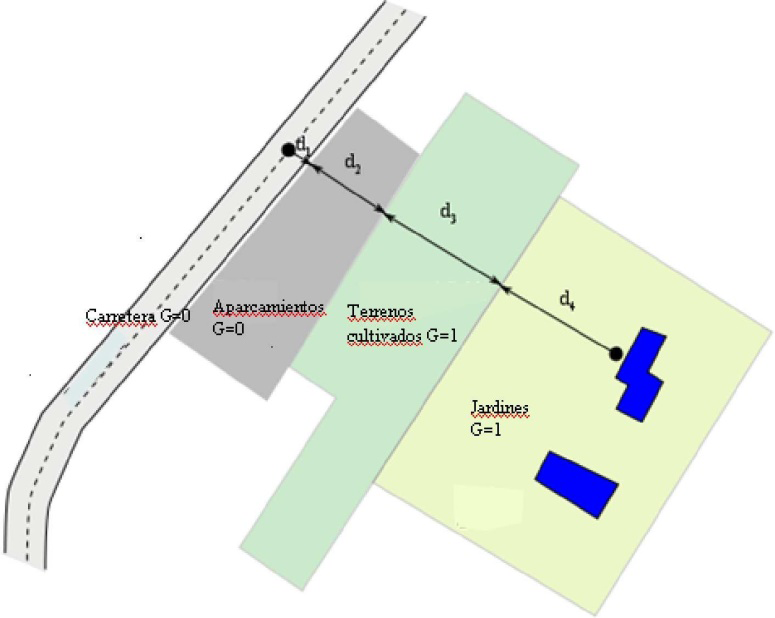
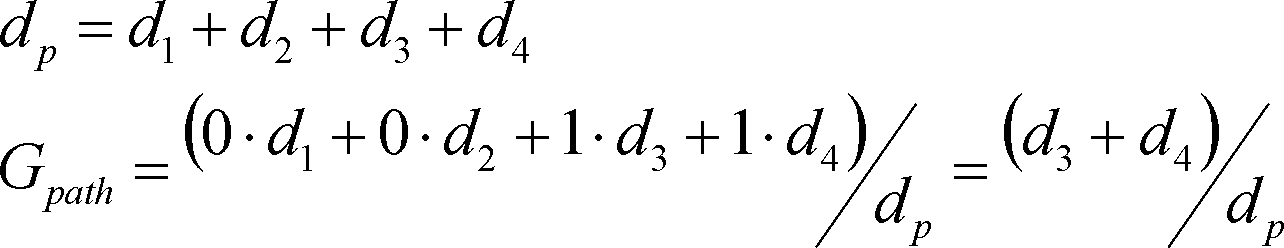
En los dos subapartados siguientes sobre los cálculos en condiciones homogéneas y favorables se presentan las notaciones genéricas y para la absorción del terreno. En el cuadro 2.5.b se ofrecen las correspondencias entre estas notaciones y las variables G_path y G′_path.

Cuadro 2.5.b

Correspondencia entre y y (G_path, G′_path)

	Condiciones homogéneas			Condiciones favorables
	Aground	Δground(S,O)	Δground(O,R)	Aground	Δground(S,O)	Δground(O,R)
	G′path		Gpath
	G′path		Gpath	G′path		Gpath

Cálculos en condiciones homogéneas.

La atenuación por el efecto suelo en condiciones homogéneas se calcula con las siguientes ecuaciones:

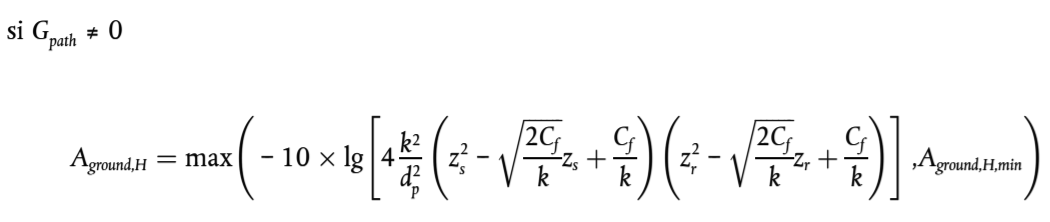
(2.5.15)

donde

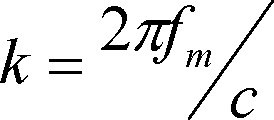
f_m es la frecuencia central nominal de la banda de frecuencias considerada, en Hz, c es la velocidad del sonido en el aire, considerada igual a 340 m/s, y C_f se define como:

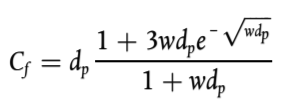
(2.5.16)

donde los valores de w se obtienen mediante la siguiente ecuación:

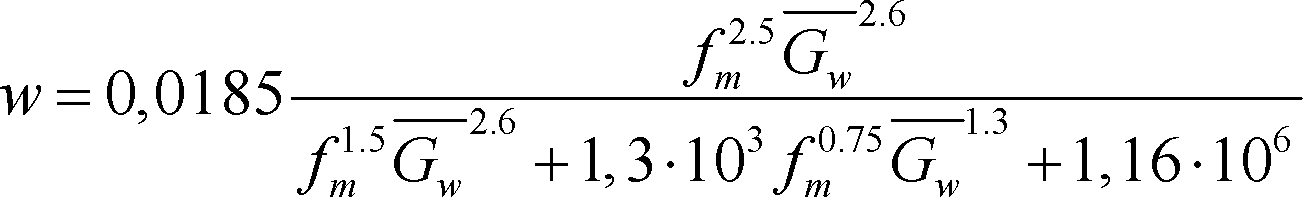
(2.5.17)

puede ser igual a G_path o G′_path, en función de si el efecto suelo se calcula con o sin difracción y según la naturaleza del terreno que se encuentra bajo la fuente (fuente real o difractada). Esto se especifica en los siguientes subapartados y se resume en el cuadro 2.5.b.

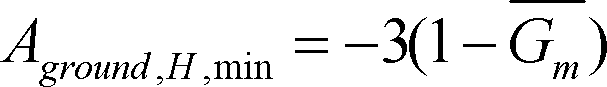
(2.5.18)

es el límite inferior de A_ground,H.

Para una trayectoria de propagación (S_i,R) en condiciones homogéneas sin difracción:

= G′_path

= G′_path

Con difracción, véase la sección sobre la difracción para las definiciones de y .

si G_path = 0: A_ground,H = – 3 dB

El término – 3(1 – ) tiene en cuenta el hecho de que, cuando la fuente y el receptor están muy alejados, la primera reflexión en lado de la fuente ya no está en la plataforma, sino sobre terreno natural.

Cálculos en condiciones favorables.

El efecto suelo en condiciones favorables se calcula con la ecuación A_ground,H, siempre que se realicen las siguientes modificaciones:

Si Gpath ≠ 0

a) En la ecuación A_ground,H, las alturas z_s y z_r se sustituyen por z_s + δ z_s + δ z_T y z_r + δ z_r + δ z_T, respectivamente, donde

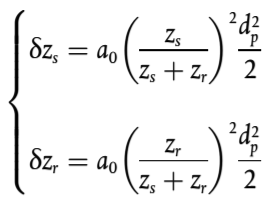
(2.5.19)

a_o = 2 × 10^–4 m^–1 es el inverso del radio de curvatura

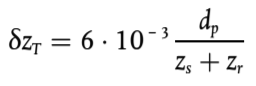
b) El límite inferior de A_ground,F depende de la geometría de la trayectoria:

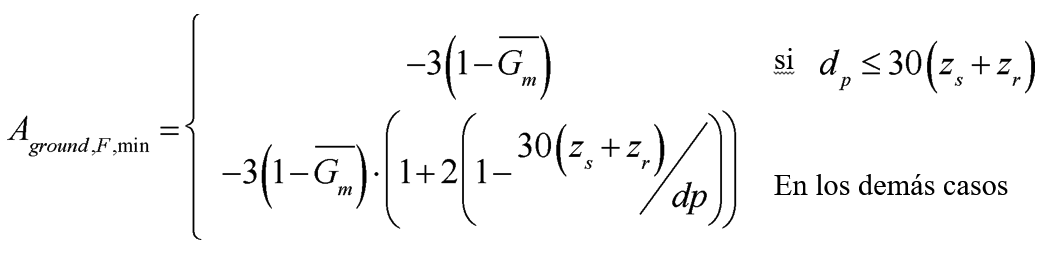
(2.2.20)

Si G_path = 0

A_ground,F = A_ground,F,min

Las correcciones de la altura δ z_s y δ z_r transmiten el efecto de la curvatura del rayo acústico. δ z_T representa el efecto de la turbulencia.

puede ser igual a G_path o G′_path, en función de si el efecto suelo se calcula con o sin difracción y según la naturaleza del terreno que se encuentra bajo la fuente (fuente real o difractada). Esto se especifica en los siguientes subapartados:

Para un trayecto (S_i,R) en condiciones favorables sin difracción:

= G_path en la ecuación (2.5.17);

= G′_path.

Con difracción, véase la sección siguiente para las definiciones de y .

Difracción.

Por norma general, la difracción debe estudiarse en la parte superior de cada obstáculo ubicado en la trayectoria de propagación. Si la trayectoria pasa a una «altura suficiente» por encima del borde de difracción, se puede definir A_dif = 0 y se puede calcular una trayectoria directa, en particular mediante la evaluación de A_ground.

En la práctica, para cada frecuencia central de la banda de frecuencias, la diferencia de la trayectoria δ se compara con la cantidad –λ/20. Si un obstáculo no produce difracción, por ejemplo si esto se puede determinar según el criterio de Rayleigh, no es necesario calcular A_dif para la banda de frecuencias considerada. En otras palabras, A_dif = 0 en este caso. De lo contrario, A_dif se calcula según se describe en las demás partes de esta sección. Esta norma se aplica tanto en condiciones homogéneas como favorables, para la difracción individual y múltiple.

Si, para una banda de frecuencias determinada, se realiza un cálculo siguiendo el procedimiento descrito en esta sección, A_ground se define como igual a 0 dB al calcular la atenuación total. El efecto suelo se tiene en cuenta directamente en la ecuación para el cálculo general de la difracción.

Las ecuaciones propuestas se usan para evaluar la difracción en pantallas delgadas, pantallas gruesas, edificios, diques de tierra (naturales o artificiales) y en los bordes de terraplenes, desmontes y viaductos.

Si se encuentran varios obstáculos con capacidad de difracción en una trayectoria de propagación, se tratan como una difracción múltiple mediante la aplicación del procedimiento descrito en la siguiente sección, que trata sobre el cálculo de la diferencia de trayecto.

Los procedimientos que aquí se describen se utilizan para calcular las atenuaciones tanto en condiciones homogéneas como favorables. La curvatura del rayo se tiene en cuenta en el cálculo de la diferencia de trayecto y para calcular los efectos suelo antes y después de la difracción.

Principios generales.

En la figura 2.5.c se ilustra el método general de cálculo de la atenuación por difracción. Este método se basa en dividir en dos la trayectoria de propagación: la trayectoria del «lado de la fuente», ubicada entre la fuente y el punto de difracción, y la trayectoria del «lado del receptor», ubicada entre el punto de difracción y el receptor.

Se calcula lo siguiente:

– un efecto suelo, en el lado de la fuente, Δ_ground(S,O)

– un efecto suelo, en el lado del receptor, Δ_ground(O,R)

– y tres difracciones:

– entre la fuente S y el receptor R: Δ_dif(S,R)

– entre la imagen de la fuente S′ y R: Δ_dif(S′,R)

– entre S y la imagen del receptor R′: Δ_dif(S,R′).

Figura 2.5.c

Geometría de un cálculo de la atenuación por difracción

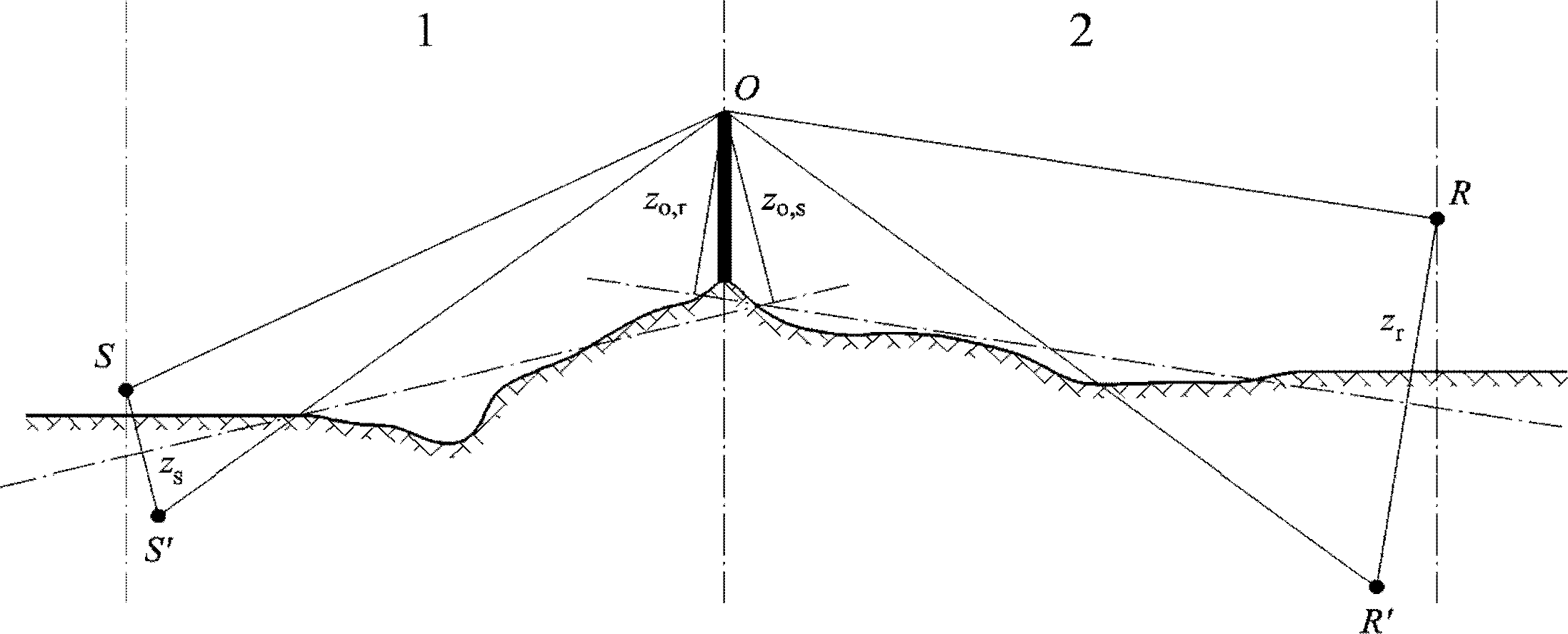
1: Lado de la fuente.

2: Lado del receptor.

donde

S es la fuente;

R es el receptor;

S' es la imagen de la fuente respecto al plano medio del suelo en el lado de la fuente;

R' es la imagen del receptor respecto al plano medio del suelo en el lado del receptor;

O es el punto de difracción;

z_s es la altura equivalente de la fuente S respecto al plano medio del suelo en el lado de la fuente;

z_o,s es la altura equivalente del punto de difracción O respecto al plano medio del suelo en el lado de la fuente

Z_r es la altura equivalente del receptor R respecto al plano medio del suelo en el lado del receptor;

z_o,r es la altura equivalente del punto de difracción O respecto al plano medio del suelo en el lado del receptor

La irregularidad del suelo entre la fuente y el punto de difracción, y entre el punto de difracción y el receptor, se tiene en cuenta mediante alturas equivalentes calculadas en relación con el plano medio del suelo, el primer lado de la fuente y el segundo lado del receptor (dos planos medios del suelo) según el método descrito en el subapartado dedicado a las alturas importantes sobre el suelo.

Difracción pura.

Para la difracción pura, sin suelo, la atenuación se calcula mediante:

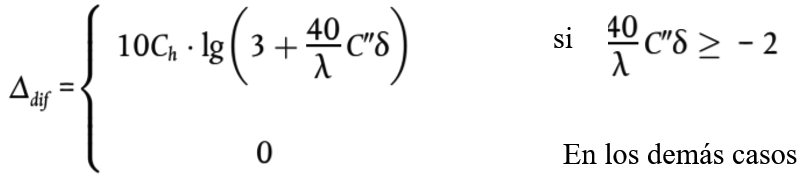
(2.5.21)

Donde:

C_h = 1

(2.5.22)

λ es la longitud de onda de la frecuencia central nominal de la banda de frecuencias considerada;

δ es la diferencia de trayecto entre la trayectoria difractado y la trayectoria directo (véase el siguiente subapartado sobre el cálculo de la diferencia de trayecto);

C" es un coeficiente utilizado para tener en cuenta difracciones múltiples:

C" = 1 para una única difracción.

Para una difracción múltiple, si e es la distancia total de la trayectoria de propagación, O1 a O2 + O2 a O3 + O3 a O4 a partir del «método de la banda elástica» (véanse las figuras 2.5.d y 2.5.f) y si e excede 0,3 m (de lo contrario, C" = 1), este coeficiente se define como:

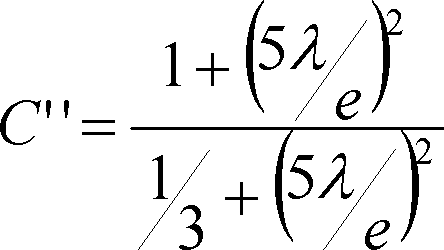
(2.5.23)

Los valores de Δ_dif deben estar limitados:

– si Δ_dif < 0: Δ_dif = 0 dB

– si Δ_dif > 25: Δ_dif = 25 dB para una difracción sobre el borde horizontal y solo sobre el término Δ_dif que figura en el cálculo de Δ_dif. Este límite superior no debe aplicarse en los términos Δ_dif que intervienen en el cálculo de Δ_ground, o para una difracción sobre un borde vertical (difracción lateral) en el caso de la cartografía del ruido industrial.

Cálculo de la diferencia de trayecto.

La diferencia de trayecto δ se calcula en un plano vertical que contiene la fuente y el receptor. Se trata de una aproximación en relación con el principio de Fermat. La aproximación continúa siendo aplicable aquí (fuentes lineales). La diferencia de trayecto δ se calcula como se ilustra en las siguientes figuras, en función de las situaciones de que se trate.

Condiciones homogéneas.

Figura 2.5.d

Cálculo de la diferencia de trayecto en condiciones homogéneas. O, O₁ y O₂ son los puntos de difracción

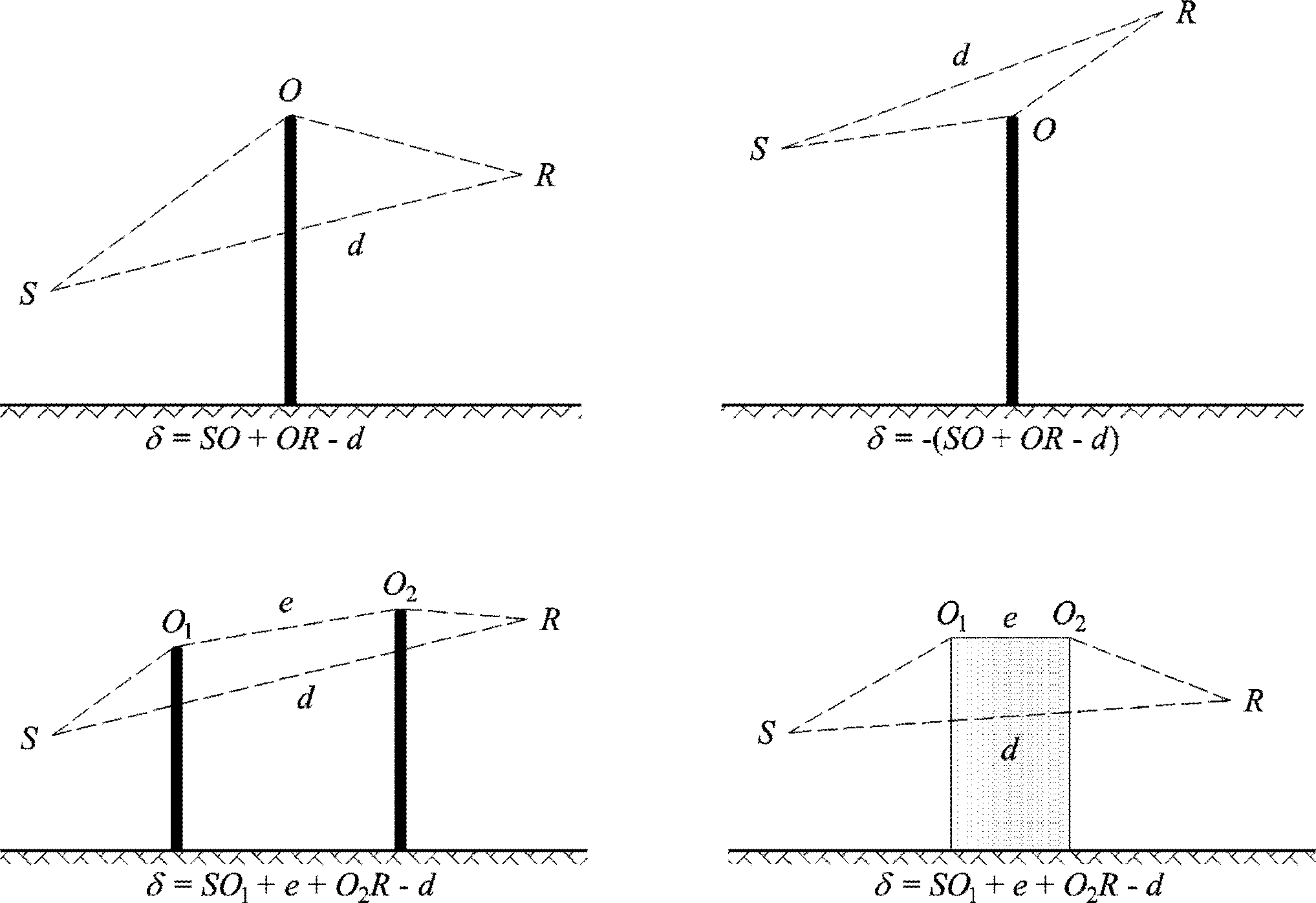
Nota: Para cada configuración, se proporciona la expresión de δ.

Condiciones favorables.

Figura 2.5.e

Cálculo de la diferencia de trayecto en condiciones favorables (difracción individual)

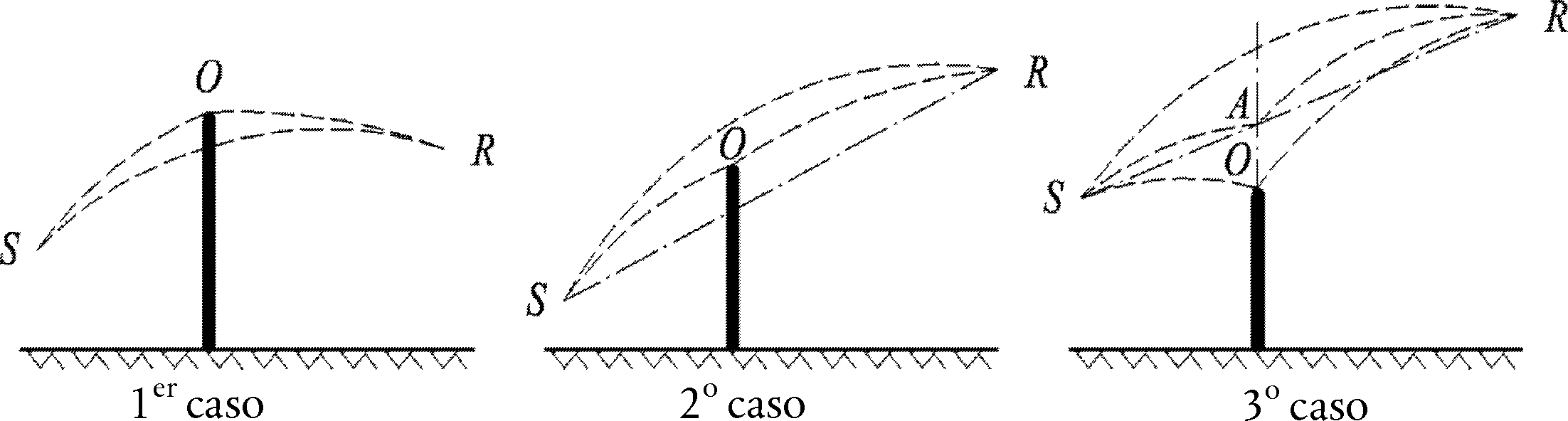
En condiciones favorables, se considera que los tres rayos de sonido curvados SO, OR y SR tienen un radio de curvatura idéntico Γ definido mediante:

Γ = max(1 000,8d)

(2.5.24)

La longitud de una curva del rayo sonoro MN se representa como en condiciones favorables. La longitud es igual a:

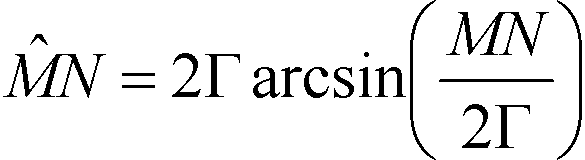
(2.5.25)

En principio, deben considerarse tres escenarios en el cálculo de la diferencia de trayecto en condiciones favorables δF (véase la figura 2.5.e). En la práctica, dos ecuaciones son suficientes:

– si el rayo sonoro recto SR es enmascarado mediante el obstáculo (primero y segundo caso de la figura 2.5.e):

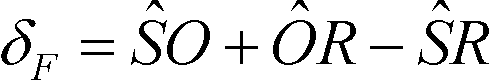
(2.5.26)

– si el rayo sonoro recto SR no es enmascarado mediante el obstáculo (tercer caso de la figura 2.5.e):

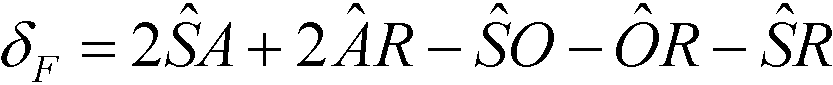
(2.5.27)

donde A es la intersección del rayo sonoro recto SR y la extensión del obstáculo difractor. Para múltiples difracciones en condiciones favorables:

– determinar la envolvente convexa definida por los diferentes bordes potenciales de difracción;

– eliminar los bordes de difracción que no se encuentran dentro del límite de la envolvente convexa;

— calcular δ_F en función de las longitudes del rayo sonoro curvado, dividiendo la trayectoria difractado en tantos segmentos curvados como sea necesario (véase la figura 2.5.f)

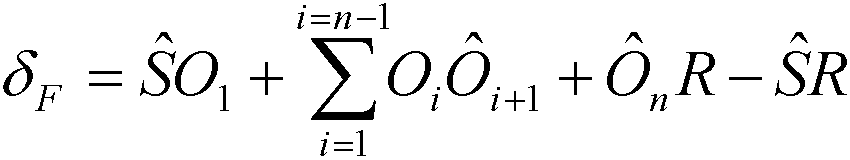
(2.5.28)

Figura 2.5.f

Ejemplo de cálculo de la diferencia de trayecto en condiciones favorables, en el caso de difracciones múltiples

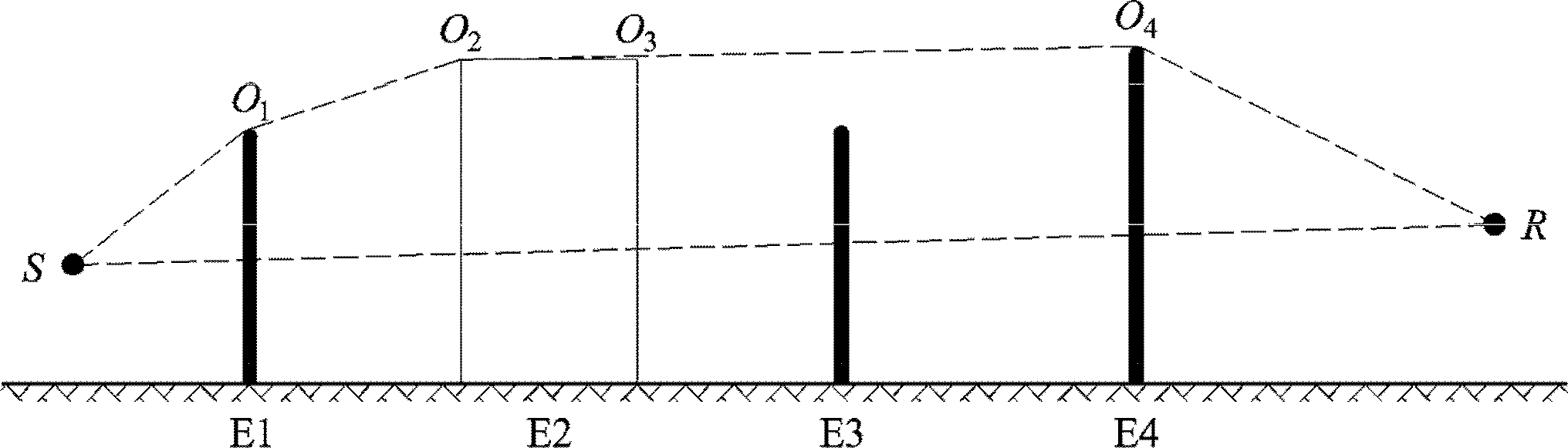
En el escenario presentado en la figura 2.5.f, la diferencia de trayecto es:

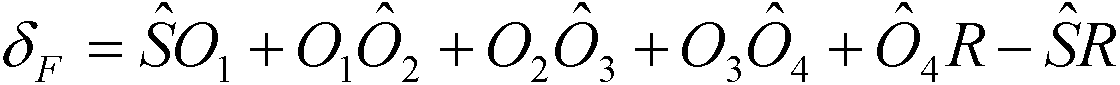
(2.2.29)

Cálculo de la atenuación A_dif.

La atenuación por difracción, teniendo en cuenta los efectos suelo en el lado de la fuente y en el lado del receptor, se calcula mediante las siguientes ecuaciones generales:

(2.5.30)

donde

– Δ_{dif (S,R)} es la atenuación por la difracción entre la fuente S y el receptor R;

– Δ_ground(S,O) es la atenuación por el efecto suelo en el lado de la fuente, ponderada mediante la difracción en el lado de la fuente; donde se entiende que O = O1 en el caso de difracciones múltiples, tal y como se ilustra en la figura 2.5.f

– Δ_ground(O,R) es la atenuación por el efecto suelo en el lado del receptor, ponderada mediante la difracción en el lado del receptor (véase el subapartado siguiente sobre el cálculo del término Δ_ground(O,R)).

Cálculo del término Δ_ground(S,O).

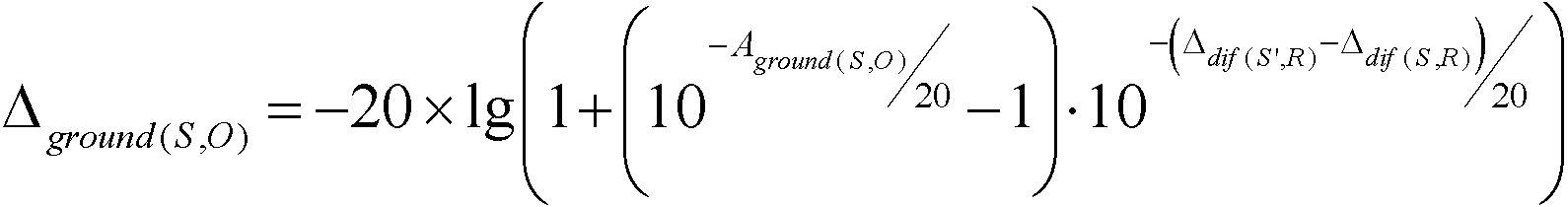
(2.5.31)

donde

– A_ground(S,O) es la atenuación por el efecto suelo entre la fuente S y el punto de difracción O. Este término se calcula como se ha indicado en el subapartado anterior relativo a los cálculos en condiciones homogéneas y en el subapartado anterior que trata sobre el cálculo en condiciones favorables, con las siguientes hipótesis:

z_r = z_o,s;

– G_path se calcula entre S y O;

– En condiciones homogéneas: = G′_path en la ecuación (2.5.17), = G′_path en la ecuación (2.5.18);

– En condiciones favorables: = G_path en la ecuación (2.5.17), = G′_path en la ecuación (2.5.20);

– Δ_dif(S′,R) es la atenuación por la difracción entre imagen de la fuente S′ y R, calculada según se ha indicado en el subapartado anterior sobre la difracción pura;

– Δ_dif(S,R) es la atenuación por la difracción entre S y R, calculada como en el subapartado VI.4.4.b.

Cálculo del término Δ_ground(O,R)

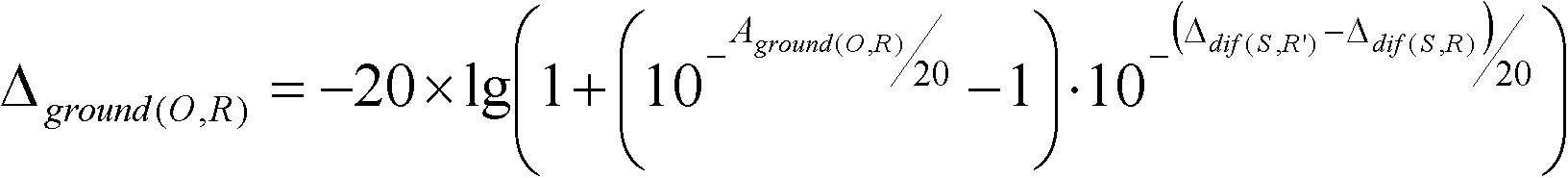
(2.5.32)

donde

– A_ground(O,R) es la atenuación por el efecto suelo entre el punto de difracción O y el receptor R. Este término se calcula como se ha indicado en el subapartado anterior relativo a los cálculos en condiciones homogéneas y en el subapartado anterior que trata sobre el cálculo en condiciones favorables, con las siguientes hipótesis:

z_s = z_o,r

– G_path se calcula entre O y R.

No es necesario tener en cuenta aquí la corrección de G′_path, ya que la fuente considerada es el punto de difracción. Por tanto, G_path debe usarse para calcular los efectos suelo, incluso para el término del límite inferior de la ecuación – 3(1 – G_path).

– En condiciones homogéneas, = G_path en la ecuación (2.5.17) y = G_path en la ecuación (2.5.18);

– En condiciones favorables, = G_path en la ecuación (2.5.17) y = G_path en la ecuación (2.5.20);

– Δ_dif(S,R′) es la atenuación por difracción entre S y la imagen del receptor R′, calculada como se ha descrito en la sección anterior relativa a la difracción pura;

– Δ_dif(S,R) es la atenuación por difracción entre S y R, calculada como se ha descrito en el subapartado anterior sobre la difracción pura.

Escenarios de bordes verticales.

La ecuación (2.5.21) puede utilizarse para calcular las difracciones en los bordes verticales (difracciones laterales) en el caso del ruido industrial. Si se da este caso, se considera A_dif = Δ_dif(S,R) y se mantiene el término A_ground. Asimismo, A_atm y A_ground deben calcularse a partir de la longitud total de la trayectoria de propagación. A_div se calcula también a partir de la distancia directa d. Las ecuaciones (2.5.8) y (2.5.6), respectivamente, son:

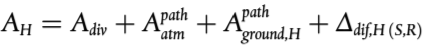
(2.5.33)

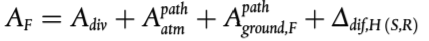
(2.5.34)

Δ_dif se utiliza en condiciones homogéneas en la ecuación (2.5.34).

Reflexión sobre obstáculos verticales.

Atenuación por absorción.

Las reflexiones sobre obstáculos verticales se tratan mediante imagen de las fuentes. Las reflexiones sobre las fachadas de los edificios y las barreras acústicas se tratan de esta forma.

Un obstáculo se considera como vertical si su inclinación en relación con la vertical es inferior a 15°.

En el caso de reflexiones sobre objetos cuya inclinación en relación con la vertical es mayor o igual a 15°, no se tiene en cuenta el objeto.

Los obstáculos en los que al menos una dimensión es inferior a 0,5 m deben ignorarse en el cálculo de la reflexión, salvo para configuraciones especiales⁵.

⁵ Una red de obstáculos pequeños en un plano y a intervalos regulares constituye un ejemplo de una configuración especial.

Nótese que las reflexiones sobre el suelo no se tratan aquí. Se tienen en cuenta en los cálculos de la atenuación debido a los límites (suelo y difracción).

Si L_WS es el nivel de potencia de la fuente S y α_r el coeficiente de absorción de la superficie del obstáculo como se define en la norma EN 1793-1:2013, entonces el nivel de potencia de la imagen de la fuente S′ es igual a:

L_WS′ = L_WS + 10 · lg(1 – α_r) = L_WS + A_refl

(2.5.35)

donde 0 ≤ α_r < 1

Las atenuaciones en la propagación descritas anteriormente se aplican a este trayecto (imagen de la fuente - receptor), como se aplican a un trayecto directo.

Figura 2.5.g

Reflexión especular sobre un obstáculo tratado mediante el método de la imagen de la fuente (S: fuente, S′: imagen de la fuente, R: receptor)

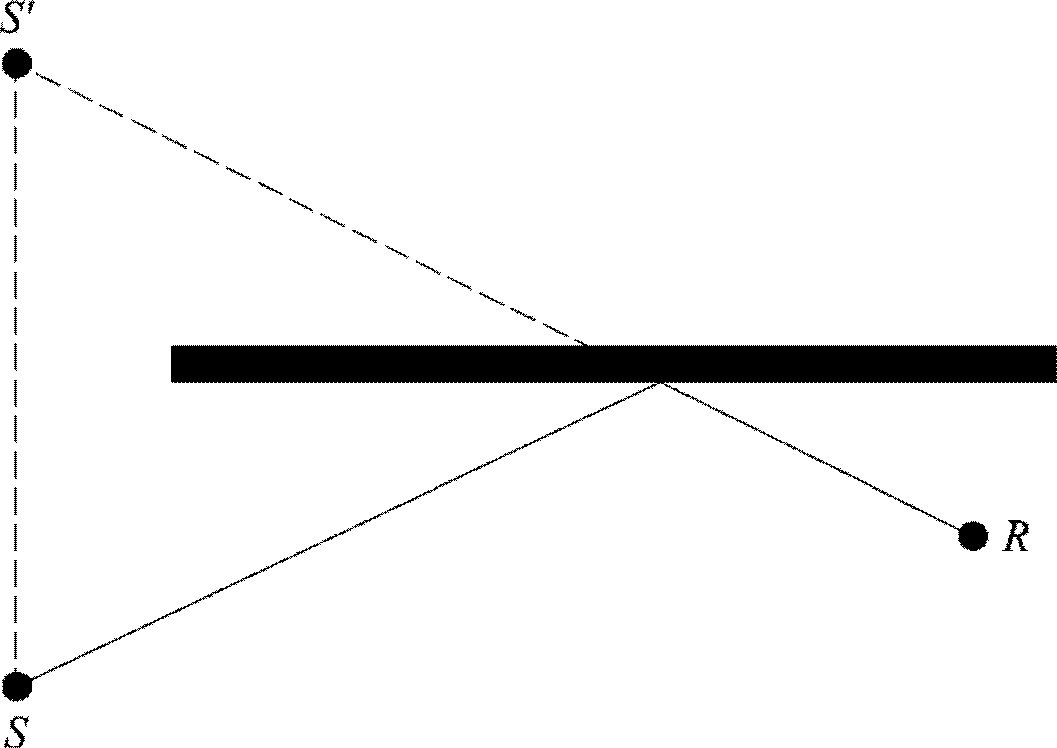
Atenuación por la retrodifracción.

En la búsqueda geométrica de trayectos acústicos, durante la reflexión en un obstáculo vertical (un muro o un edificio), la posición del impacto del rayo en relación con el borde superior de este obstáculo determina la proporción más o menos importante de la energía reflejada efectivamente. Esta pérdida de energía sonora cuando el rayo experimenta una reflexión se denomina atenuación a través de la retrodifracción.

En caso de que se den posibles reflexiones múltiples entre dos muros verticales, al menos debe tenerse en cuenta la primera reflexión.

Si se trata de una trinchera (véase, por ejemplo, la figura 2.5.h), la atenuación por retrodifracción debe aplicarse a cada reflexión en los muros de contención.

Figura 2.5.h

Rayo sonoro reflejado en el orden de 4 en una pista de una vía en trinchera: sección transversal real (arriba) y sección transversal desplegada (abajo)

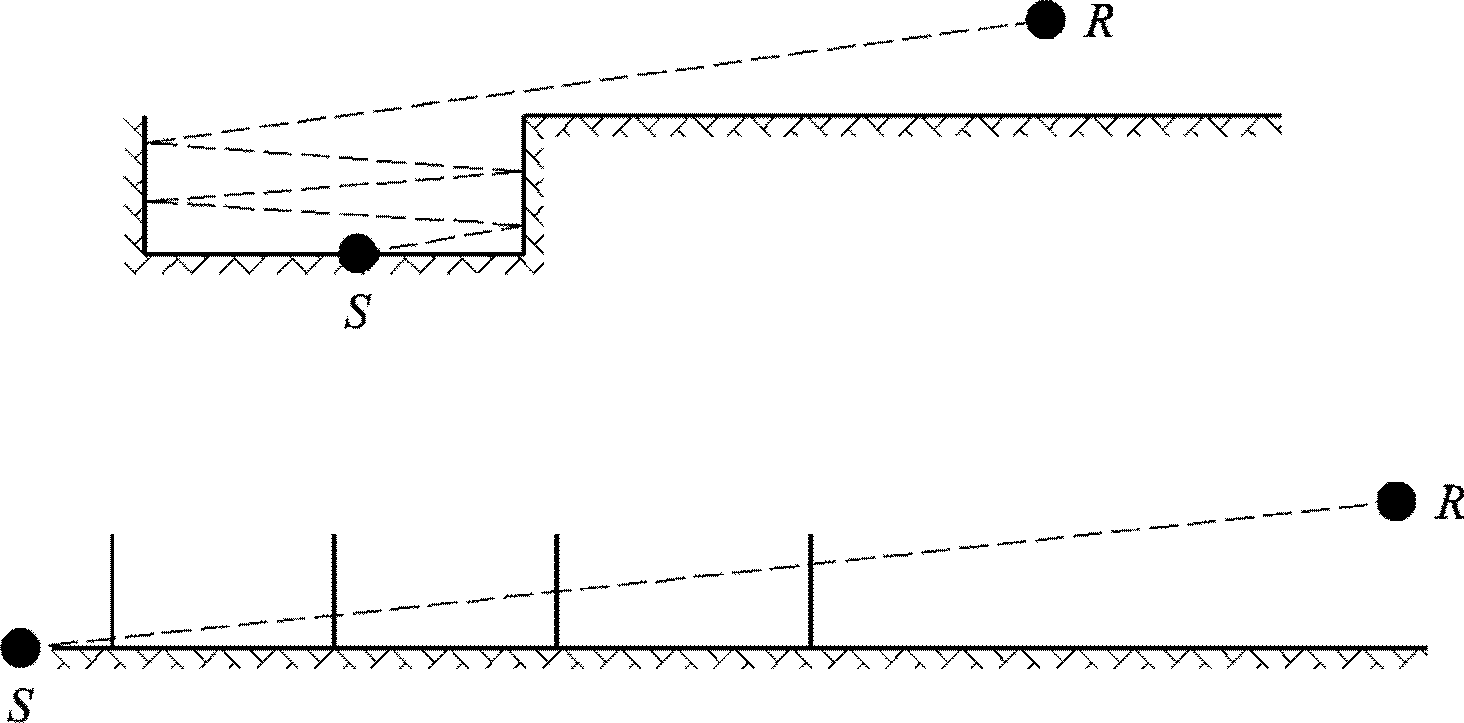
En esta representación, el rayo sonoro alcanza el receptor «pasando posteriormente a través de» los muros de contención de la zanja, que, por tanto, se puede comparar con las aperturas.

Al calcular la propagación a través de una apertura, el campo acústico en el receptor es la suma del campo directo y el campo difractado por los bordes de la apertura. Este campo difractado garantiza la continuidad de la transición entre el área libre y el área sombreada. Cuando el rayo alcanza el borde de la apertura, el campo directo se atenúa. El cálculo es idéntico al de la atenuación mediante una barrera en el área libre.

La diferencia de trayecto δ′ asociada con cada retrodifracción es lo opuesto de la diferencia de trayecto entre S y R con respecto a cada borde superior O, en una sección transversal desplegada (véase la figura 2.5.i).

δ′ = – (SO + OR – SR)

(2.5.36)

Figura 2.5.i

La diferencia de trayecto para la segunda reflexión

El signo «menos» de la ecuación (2.5.36) significa que el receptor se tiene en cuenta aquí en el área libre.

La atenuación a través de la retrodifracción Δ_retrodif se obtiene mediante la ecuación (2.5.37), que es similar a la ecuación (2.5.21) con notaciones reformuladas.

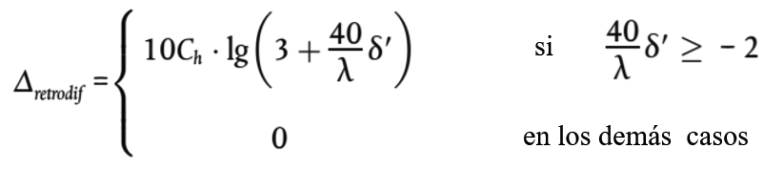
(2.5.37)

Esta atenuación se aplica al rayo directo cada vez que «pasa a través» (se refleja) de un muro o edificio. El nivel de potencia de la imagen de la fuente S′ es:

L_W′ = L_W + 10 × lg(1 – αr) – Δ_retrodif

(2.5.38)

En configuraciones de propagación complejas, pueden existir difracciones entre reflexiones, o bien entre el receptor y las reflexiones. En este caso, la retrodifracción de los muros se calcula al considerar la trayectoria entre la fuente y el primer punto de difracción R′ (considerado por tanto como el receptor en la ecuación (2.5.36)). Este principio se ilustra en la figura 2.5.j.

Figura 2.5.j

La diferencia de trayecto con presencia de una difracción: sección transversal real (arriba) y sección transversal desplegada (abajo)

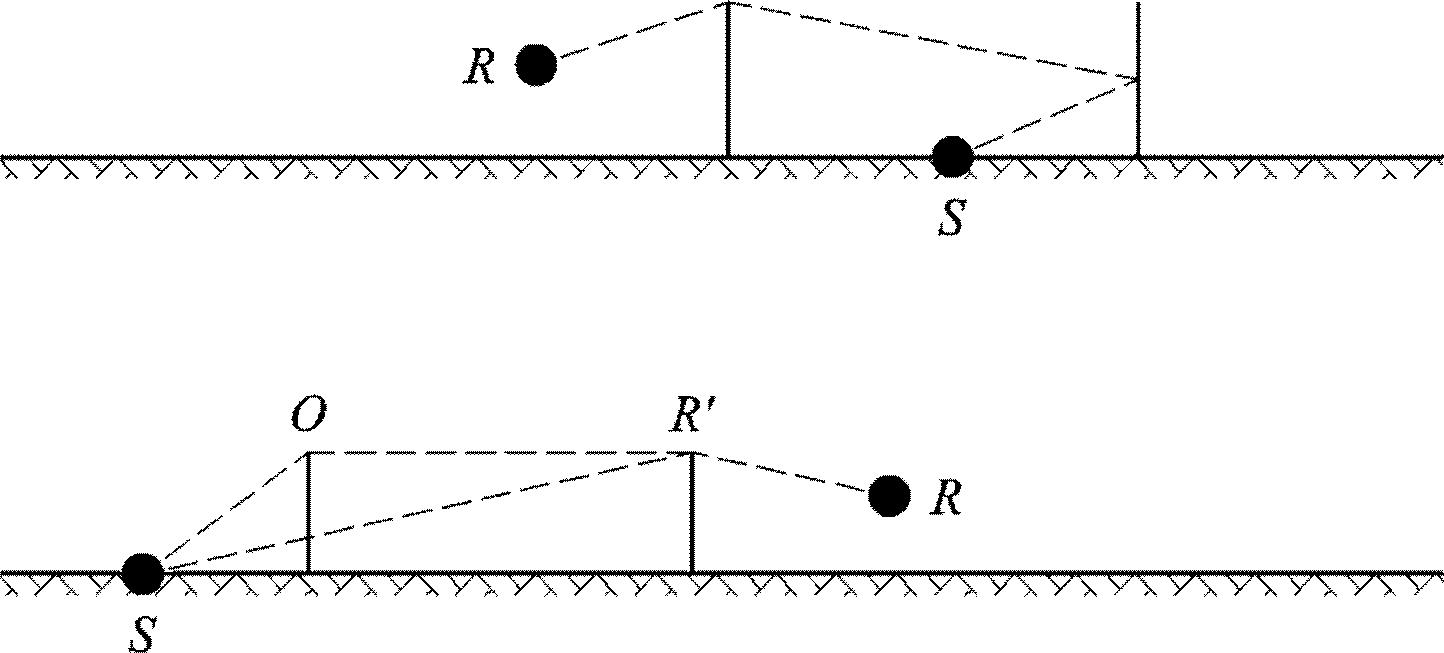
En caso de reflexiones múltiples, se añaden las reflexiones por cada reflexión individual.

2.6. Disposiciones generales — Ruido de aeronaves.

2.6.1. Definiciones y símbolos.

Aquí se describen algunos términos importantes atribuyéndoles significados generales en este documento. La lista no es completa; de hecho, solo se incluyen expresiones y acrónimos utilizados con frecuencia. Otros se describen la primera vez que aparecen.

Los símbolos matemáticos (que aparecen después de los términos) son los símbolos principales que se utilizan en las ecuaciones en el texto principal. Otros símbolos utilizados localmente en el texto y en los apéndices se definen cuando se usan.

Al lector se le recuerda periódicamente la intercambiabilidad de las palabras sonido y ruido en este documento. Aunque la palabra ruido tiene connotaciones subjetivas –los técnicos acústicos suelen definirlo como «sonido interferente»– en el campo del control de ruido de aeronaves suele considerarse solo como sonido –energía aérea transmitida por el movimiento de las ondas sonoras–. El símbolo -> denota referencias cruzadas a otros términos incluidos en la lista.

Definiciones.

AIP	Publicación de información aeronáutica.
Configuración de la aeronave	Posición de los slats, los flaps y los trenes de aterrizaje.
Movimientos de aeronaves	Un aterrizaje, un despegue u otra acción de la aeronave que afecta a la exposición al ruido en torno a un aeródromo.
Datos de ruido y rendimiento (performance) de las aeronaves	Datos que describen las características acústicas y de rendimiento (performance) de los diferentes tipos de aviones necesarios para el proceso de modelización. Incluyen las -> curvas NPD e información que permite calcular la potencia o el empuje del reactor como una función de la -> configuración del vuelo. Los datos suele facilitarlos el fabricante de la aeronave, aunque cuando no es posible, a veces se obtienen de otras fuentes. Si no hay datos disponibles, es habitual representar la aeronave de que se trate adaptando los datos para una aeronave convenientemente similar –a esto se hace referencia con el término sustitución–.
Altitud	Altura por encima del nivel medio del mar.
Base de datos ANP	La base de datos del ruido y el rendimiento de las aeronaves se incluye en el apéndice I.
Nivel sonoro con ponderación A,	LA Escala básica de nivel de sonido/ruido utilizada para medir el ruido ambiental, incluido el que generan las aeronaves y en el que se basan la mayoría de las métricas de las curvas de nivel de ruido (isófonas).
Trayectoria principal en tierra	Una línea representativa o ruta nominal que define el centro de una banda de dispersión de trayectorias.
Nivel del evento sonoro de la línea base	El nivel del evento sonoro que figura en una base de datos NPD.
Liberación del freno	Punto de partida de rodaje
Empuje neto corregido	En un reglaje de la potencia determinado (por ejemplo, EPR o N1), el empuje neto disminuye al disminuir la densidad del aire por lo que aumenta al aumentar la altitud del aeroplano; el empuje neto corregido es el valor al nivel del mar.
Nivel de sonido/ruido acumulado	Una medida en decibelios del ruido recibido durante un período de tiempo específico, en un punto cercano a un aeropuerto, con tráfico aéreo en condiciones de funcionamiento y trayectorias de vuelo normales. Se calcula mediante la acumulación, de los niveles de sonido/ruido del evento que se producen en dicho punto.
Suma o promedio de decibelios	A veces se denomina suma o media energética o logarítmica (en oposición a los valores aritméticos). Se utiliza para sumar o calcular el promedio de cantidades expresadas en niveles; por ejemplo, la suma de decibelios: =
Fracción de energía, F	Relación entre la energía acústica recibida del segmento y la energía recibida de la trayectoria de vuelo infinita.
Reglaje de potencia del motor	Valor del -> parámetro de potencia relacionado con el ruido utilizado para determinar la emisión de ruido que figura en la base de datos NPD.
Nivel sonoro continuo equivalente, L eq	Una medida del sonido a largo plazo. Es el nivel sonoro de un sonido continuo estable, que durante un período de tiempo específico, contiene la misma energía total que el sonido variable real.
Nivel de sonido/ruido del evento	Una medida en decibelios de la energía acústica recibida por el paso de un avión -> nivel de exposición al ruido.
Configuración del vuelo	= -> Configuración de la aeronave + -> Parámetros del vuelo.
Parámetros del vuelo	Reglaje de la potencia de la aeronave, velocidad, ángulo de alabeo y peso.
Trayectoria del vuelo	La trayectoria de un avión en el aire, definida en tres dimensiones, normalmente con referencia a un origen en el punto de la carrera de despegue o en el umbral de aterrizaje.
Segmento de la trayectoria del vuelo	Parte de la trayectoria del vuelo de una aeronave representada a efectos de modelización acústica mediante una línea recta de longitud finita.
Procedimiento del vuelo	La secuencia de pasos operativos que sigue la tripulación o el sistema de gestión del vuelo expresada como cambios de la configuración del vuelo como una función de distancia a lo largo de la trayectoria en tierra.
Perfil del vuelo	Variación de la altura del avión a lo largo de la trayectoria en tierra (a veces también incluye cambios de -> configuración del vuelo), que se describe como un conjunto de -> puntos del perfil.
Plano de tierra	(O tierra nominal) Superficie de tierra horizontal a través del punto de referencia del aeródromo en el que se suelen calcular las curvas de nivel de ruido.
Velocidad respecto al suelo	Velocidad del aeroplano relativa a un punto fijo en el suelo.
Trayectoria en tierra	Proyección vertical de la trayectoria de vuelo en el plano de tierra.
Altura	Distancia vertical entre el avión y el -> plano de tierra.
Nivel sonoro integrado	También denominado -> nivel de exposición sonora de evento simple.
ISA	Atmósfera tipo internacional definida por la OACI. Define la variación de la temperatura del aire, la presión y la densidad con la altura sobre el nivel medio del mar. Se utiliza para normalizar los resultados de los cálculos de diseño del avión y el análisis de los datos de prueba.
Atenuación lateral	Exceso de atenuación del sonido con una distancia atribuible, directa o indirectamente, a la presencia de la superficie del terreno. Importante a ángulos bajos de elevación (del aeroplano por encima del plano de tierra).
Nivel sonoro de ruido máximo	El nivel sonoro máximo alcanzado durante un evento.
Nivel medio del mar, MSL	La elevación estándar de la superficie terrestre a la que hace referencia la -> ISA.
Empuje neto	La fuerza propulsora ejercida por un motor en el fuselaje.
Ruido	El ruido se define como sonido no deseado. No obstante, las métricas como el nivel sonoro con ponderación A (LA) y el nivel efectivo de ruido percibido (EPNL) efectivamente convierten los niveles sonoros en niveles de ruido. A pesar de la consecuente falta de rigor, los términos sonido y ruido a veces se usan indistintamente en este documento, como en otras partes, sobre todo en combinación con la palabra nivel.
Curvas de nivel sonoro / (Isófonas)	Una línea del valor constante del nivel sonoro / de ruido acumulado de las aeronaves en torno a un aeropuerto.
Impacto del ruido	Los efectos adversos del ruido en los receptores; las métricas del ruido son indicadores del impacto del ruido.
Índice de ruido	Una medida del sonido a largo plazo o acumulativo que está relacionado con (es decir, se considera una variable explicativa de) sus efectos adversos en las personas. Puede tener en cuenta en cierta medida algunos factores además de la magnitud del sonido (en particular la hora del día). Un ejemplo es el nivel día-tarde-noche LDEN.
Nivel de ruido	Una medida de sonido en decibelios en una escala que indica su sonoridad o su ruidosidad. En el caso del ruido ambiental originado por las aeronaves, suelen utilizarse dos escalas: Nivel sonoro con ponderación A y nivel de ruido percibido. Estas escalas aplican diferentes ponderaciones al sonido de distintas frecuencias, a fin de simular la percepción humana.
Índice de ruido	Una expresión utilizada para describir cualquier medida de la cantidad de ruido en la posición de un receptor, independientemente de que se trate de un único evento o de una acumulación de ruidos durante un tiempo prolongado. Hay dos medidas del ruido de un único evento que se usan habitualmente: el nivel máximo alcanzado durante el evento, o bien su nivel de exposición al ruido, una medida de su energía acústica total determinada por la integración temporal.
Datos/relaciones ruido-potencia distancia (NPD)	Niveles sonoros de un evento tabulados en función de la distancia por debajo de un aeroplano en un vuelo de nivel constante a una velocidad de referencia en una atmósfera de referencia, para cada uno de los -> configuración de la potencia del motor. Los datos tienen en cuenta los efectos de la atenuación acústica por propagación de la onda esférica (ley de la inversa de los cuadrados de la distancia) y la absorción atmosférica. La distancia se define como perpendicular a la trayectoria de vuelo del aeroplano y al eje aerodinámico del ala del avión (es decir, en vertical por debajo del avión en vuelos sin alabeo).
Parámetro de potencia relacionada con el ruido	Parámetro que describe o indica el esfuerzo de propulsión generado por el motor de una aeronave con el que se puede relacionar de manera lógica la emisión de potencia acústica, que por lo general se denomina -> empuje neto corregido. En este texto, en general se le denomina «potencia» o «reglaje de la potencia».
Significancia del ruido	La contribución del segmento de la trayectoria del vuelo es «significante desde el punto de vista del ruido» si afecta al nivel de ruido del evento en la medida en que resulte apreciable. Ignorar los segmentos que no revisten importancia desde el punto de vista del ruido produce ahorros masivos en el procesamiento por ordenador.
Observador	-> Receptor.
Etapas del procedimiento	Prescripción de un perfil de vuelo (los pasos incluyen cambios de velocidad o altitud).
Punto del perfil	Altura del punto final del segmento de la trayectoria del vuelo (en un plano vertical sobre la trayectoria en tierra).
Receptor	Un receptor del ruido que llega desde una fuente; principalmente en un punto en la superficie del terreno o próxima a ella.
Atmósfera de referencia	Una tabulación de parámetros de absorción del ruido utilizada para normalizar los datos de NPD (véase el apéndice D).
Día de referencia	Un conjunto de condiciones atmosféricas conforme a las cuales se normalizan los datos de ANP.
Duración de referencia	Un intervalo de tiempo nominal utilizado para normalizar las medidas del nivel de exposición al ruido de un único evento; igual a 1 segundo en el caso de -> SEL.
Velocidad de referencia	Velocidad del aeroplano respecto al suelo conforme a la cual se normalizan los datos SEL de -> NPD.
SEL	->Nivel de exposición al ruido.
Nivel de exposición al ruido de evento simple	El nivel de sonido que tendría un evento si toda su energía acústica se comprimiera de manera uniforme en un intervalo de tiempo estándar conocido como la -> duración de referencia
Terreno blando	Una superficie del terreno que, en términos acústicos, es «blanda», por lo general el suelo cubierto de hierba, que rodea a la mayoría de los aeródromos. Las superficies del terreno acústicamente duras, es decir, altamente reflectantes, incluyen el hormigón y el agua. La metodología de obtención de las curvas de ruido descrita aquí se aplica a las condiciones de superficies blandas.
Sonido	Energía transmitida a través del aire mediante el movimiento ondulatorio (longitudinal) que es percibida por el oído.
Atenuación acústica	La reducción de la intensidad del sonido con la distancia a lo largo de la trayectoria de propagación. Entre sus causas en el caso del ruido de aeronaves destacan la propagación ondulatoria esférica, la absorción atmosférica y la -> atenuación lateral.
Exposición al ruido	Una medida de inmisión de energía acústica total durante un período de tiempo.
Nivel de exposición al ruido, LAE (Acrónimo SEL)	Una métrica normalizada en la ISO 1996-1 o en la ISO 3891 = Un nivel de exposición al ruido de un evento simple con ponderación A con referencia a 1 segundo.
Intensidad acústica	La intensidad de la inmisión acústica en un punto se relaciona con la energía acústica (e indicada mediante niveles sonoros medidos).
Nivel sonoro	Una medida de energía acústica expresada en unidades de decibelio. El sonido recibido se mide con o sin «ponderación de frecuencia»; a los niveles medidos con una ponderación determinada a menudo se les denomina -> niveles de ruido
Longitud de la etapa o del viaje	Distancia hasta el primer destino de la aeronave que despega; se considera como un indicador del peso de la aeronave.
Punto de partida de rodaje, SOR	El punto de la pista desde el cual una aeronave empieza a despegar. También se le denomina «liberación del freno».
Velocidad real	Velocidad real de la aeronave en relación con el aire (= velocidad respecto al suelo con aire en calma).
Nivel de sonido continuo equivalente corregido, Leq,W	Una versión modificada de Leq en la que se asignan diferentes ponderaciones al ruido que se produce durante diferentes períodos del día (normalmente durante el día, la tarde y la noche).

Símbolos:

d	Distancia más corta desde un punto de observación hasta un segmento de la trayectoria del vuelo.
dp	Distancia perpendicular desde un punto de observación hasta la trayectoria de vuelo (distancia oblicua).
dλ	Distancia a escala.
Fn	Empuje neto real por motor.
Fn/δ	Empuje neto corregido por motor.
h	Altitud de la aeronave (por encima de MSL).
L	Nivel de ruido del evento (escala indefinida).
L(t)	Nivel sonoro en el intervalo de tiempo t (escala indefinida).
LA, LA(t)	Un nivel de presión sonora ponderado A (en el intervalo de tiempo t), medido con ponderación temporal slow.
LAE	(SEL) Nivel de exposición al ruido.
LAmax	Valor máximo de LA(t) durante un evento.
LE	Nivel de exposición al ruido de evento simple.
LE∞	Nivel de exposición al ruido de evento simple determinado en la base de datos NPD.
LEPN	Nivel efectivo de ruido percibido.
Leq	Nivel sonoro continuo equivalente.
Lmax	Valor máximo de L(t) durante un evento.
Lmax,seg	Nivel máximo generado por un segmento.
L	Distancia perpendicular desde un punto de observación hasta la trayectoria en tierra.
lg	Logaritmo en base 10.
N	Número de segmentos o subsegmentos.
NAT	Número de eventos en los que Lmax excede un umbral específico.
P	Parámetro de potencia en la variable de NPD L(P,d).
Pseg	Parámetro de potencia relativo a un segmento concreto.
q	Distancia desde el inicio del segmento hasta el punto de aproximación máxima.
R	Radio de giro.
S	Desviación estándar.
s	Distancia a lo largo de la trayectoria en tierra.
sRWY	Longitud de la pista.
t	Tiempo.
te	Duración efectiva de un único evento sonoro.
t0	Tiempo de referencia para el nivel de sonido integrado.
V	Velocidad respecto a tierra.
Vseg	Velocidad respecto a tierra de segmento equivalente.
Vref	Velocidad respecto a tierra de referencia para la que se definen los datos de NPD.
x,y,z	Coordenadas locales.
x′,y′,z′	Coordenadas de la aeronave.
XARP, YARP, ZARP	Posición del punto de referencia del aeródromo en coordenadas geográficas.
z	Altura de la aeronave por encima del plano de tierra o del punto de referencia del aeródromo.
α	Parámetro utilizado para calcular la corrección para el segmento finito ΔF.
β	Ángulo de elevación de la aeronave con respecto al plano de tierra.
ε	Ángulo de alabeo de la aeronave.
γ	Ángulo de subida/bajada.
φ	Ángulo de depresión (parámetro de directividad lateral).
λ	Longitud total del segmento.
ψ	Ángulo entre la dirección del movimiento de la aeronave y la dirección hacia el observador.
ξ	Rumbo de la aeronave, medido en sentido de las agujas del reloj desde el norte magnético.
Λ(β,ℓ)	Atenuación lateral aire-tierra.
Λ(β)	Atenuación lateral aire-tierra a larga distancia.
Γ(ℓ)	Factor de distancia de atenuación lateral.
Δ	Cambio de valor de una cantidad o una corrección (como se indica en el texto).
ΔF	Corrección de segmento finito.
ΔI	Corrección de la instalación del motor.
Δi	Ponderación para el tiempo i durante el día, en dB.
Δrev	Reversa.
ΔSOR	Corrección del punto de partida de rodaje.
ΔV	Corrección de la duración (velocidad).

Subíndices:

1, 2	Subíndices que denotan los valores iniciales y finales de un intervalo o segmento.
E	Exposición.
i	Índice de la suma de categorías/tipos de aeronaves.
j	Índice de la suma de la trayectoria en tierra/subtrayectoria.
k	Índice de la suma de segmentos.
max	Máximo.
ref	Valor de referencia.
seg	Valor específico del segmento.
SOR	En relación con el punto de partida de rodaje.
TO	Despegue.

2.6.2. Marco de calidad.

Precisión de los valores de entrada.

Todos los valores de entrada que afecten al nivel de emisiones de una fuente, incluida la posición de la fuente, se determinarán al menos con una precisión correspondiente a una incertidumbre de ± 2dB(A) en el nivel de emisiones de la fuente (dejando invariables todos los demás parámetros).

Uso de los valores predeterminados.

Al aplicar el método, los datos de entrada reflejarán el uso real. En general, no se utilizarán valores de entrada predeterminados ni estimados. En particular, las trayectorias de vuelo se obtendrán de los datos de radar siempre que existan y que sean de la calidad suficiente. Se aceptan estimaciones y valores de entrada predeterminados, por ejemplo, para rutas modelizadas utilizadas en lugar de trayectorias de vuelo obtenidas por radar, si la recopilación de datos reales implica costes sumamente desproporcionados.

Calidad del software usado para los cálculos.

El software utilizado para realizar los cálculos deberá acreditar la conformidad con los métodos aquí descritos mediante una certificación de resultados derivados de los ensayos realizados.

El software utilizado para el cálculo de los niveles de ruido en el ambiente exterior deberá cumplir con los requerimientos establecidos en la norma ISO 17534 en lo referente a calidad y garantía de calidad acústica y a las recomendaciones generales para los ensayos (test) e interface de control de calidad, así como las recomendaciones para la aplicación del control de calidad en la ejecución de los métodos descritos en este anexo por el software de acuerdo con la norma ISO 17534-1.

2.7. Ruido de aeronaves.

2.7.1. Objetivo y ámbito de aplicación del documento.

Los mapas de isófonas o curvas de nivel de ruido se usan para indicar el alcance y la magnitud del impacto del ruido de aeronaves en los aeropuertos, y este impacto se indica mediante los valores de un índice o una métrica de ruido especificados. Una isófona es una línea a lo largo de la cual el valor del índice de ruido es constante. El valor de índice tiene en cuenta todos los eventos de ruido de aeronaves individuales que ocurren durante algún período específico de tiempo, que suele medirse en días o meses.

El ruido en los puntos sobre el terreno originado por el vuelo de las aeronaves que entran y salen de un aeródromo cercano depende de muchos factores. Entre ellos, los principales son los tipos de aeronave y su sistema motopropulsor; los procedimientos de gestión de la potencia, los flaps y la velocidad aerodinámica utilizados en los aeroplanos; las distancias desde los puntos afectados hasta las diferentes trayectorias de vuelo; y las condiciones meteorológicas y la topografía locales. Las operaciones aeroportuarias por lo general incluyen diferentes tipos de aviones, varios procedimientos de vuelo y un rango de pesos operacionales.

Las curvas de nivel de ruido se generan mediante el cálculo matemático de los valores del índice de ruido locales. En este documento se explica detalladamente cómo calcular, en un punto de observación, los niveles de eventos de ruido de aeronaves individuales, cada uno de ellos para el vuelo de una aeronave específica o un tipo de vuelo, que posteriormente son promediados, o bien se acumulan, para obtener los valores del índice en dicho punto. Los valores requeridos del índice de ruido se obtienen mediante la repetición de los cálculos según resulte necesario para diferentes movimientos de los aviones, procurando maximizar la eficiencia excluyendo eventos que no «son significativos desde el punto de vista del ruido» (es decir, que no contribuyen significativamente al ruido total).

Cuando las actividades que generan ruidos asociadas con operaciones aeroportuarias no contribuyen sustancialmente a la exposición global de la población al ruido de aeronaves y a las curvas de nivel de ruido asociadas, estas pueden excluirse. Estas actividades incluyen: helicópteros, rodaje, prueba de motores y uso de fuentes de energía auxiliares. Esto no significa necesariamente que su impacto resulte insignificante y, cuando se dan estas circunstancias, se puede realizar una evaluación de las fuentes, según se describe en los apartados 2.7.21 y 2.7.22.

2.7.2. Esquema del documento.

El proceso de generación de las curvas de nivel de ruido se ilustra en la figura 2.7.a. Las isófonas se obtienen para varios propósitos y tienden a controlar los requisitos de las fuentes y el tratamiento previo de los datos de entrada. Las curvas de nivel de ruido que representan el impacto histórico del ruido deberán obtenerse de los registros reales de las operaciones de las aeronaves ‒de movimientos, pesos, trayectorias de vuelo medidas por radar, etc.‒. Las curvas utilizadas para la planificación de situaciones dependen más de las previsiones ‒de tráfico y trayectorias de vuelo y de las características de rendimiento y ruido de futuras aeronaves‒.

Figura 2.7.a

Proceso de generación de las curvas de nivel de ruido

Independientemente de la fuente de los datos de vuelo, cada movimiento diferente de la aeronave, llegada o salida, se define en términos de la geometría de la trayectoria de vuelo y de la emisión de ruido de la aeronave a medida que sigue dicha trayectoria (los movimientos que son prácticamente iguales en términos de ruido y trayectoria de vuelo se incluyen mediante una multiplicación sencilla). La emisión de ruido depende de las características de la aeronave ‒principalmente de la potencia que generan sus motores‒. La metodología recomendada implica dividir la trayectoria de vuelo en segmentos. En las secciones 2.7.3 a 2.7.6 se describen los elementos de la metodología y se explica el principio de segmentación en el que se basa; el nivel de ruido del evento observado es una agregación de las contribuciones de todos los segmentos «significativos desde el punto de vista del ruido» de la trayectoria de vuelo, cada uno de los cuales se puede calcular con independencia del resto. En las secciones 2.7.3 a 2.7.6 también se describen los requisitos de los datos de entrada para calcular un conjunto de isófonas de ruido. Las especificaciones detalladas de los datos operativos necesarios se describen en el apéndice A.

La forma en que se calculan los segmentos de la trayectoria de vuelo a partir de los datos de entrada procesados previamente se describe en las secciones 2.7.7 a 2.7.13. Esto implica la aplicación de análisis del rendimiento (performance) del vuelo de la aeronave, y las ecuaciones para ello se detallan en el apéndice B. Las trayectorias de vuelo están sujetas a una variabilidad importante ‒las aeronaves que siguen cualquier ruta se dispersan en abanico debido a los efectos de las diferencias en las condiciones atmosféricas, el peso de las aeronaves y los procedimientos de funcionamiento, las limitaciones de control del tráfico aéreo, etc. Esto se tiene en cuenta mediante la descripción estadística de cada trayectoria de vuelo ‒como una trayectoria central o «principal» acompañada de un conjunto de trayectorias dispersas‒. Esto también se explica en las secciones 2.7.7 a 2.7.13 con referencia a información adicional que consta en el apéndice C.

En las secciones 2.7.14 a 2.7.19 se describen los pasos que hay que seguir para calcular el nivel de ruido de un único evento ‒el ruido generado en un punto sobre el terreno por el movimiento de una aeronave‒. En el apéndice D se trata la realización de nuevos cálculos de los datos de NPD para condiciones distintas de las de referencia. En el apéndice E se explica la fuente de dipolo acústico utilizada en el modelo para definir la radiación de sonido desde los segmentos de la trayectoria de vuelo de longitud finita.

Las aplicaciones de las relaciones de modelización descritas en los capítulos 3 y 4 requieren, aparte de las trayectorias de vuelo pertinentes, datos apropiados sobre el ruido y el rendimiento de la aeronave en cuestión.

El cálculo fundamental consiste en determinar el nivel de ruido del evento para un único movimiento de la aeronave en un único punto de observación. Esto debe repetirse para todos los movimientos de la aeronave en el conjunto de puntos establecido, abarcando el alcance esperado de las curvas de nivel de ruido requeridas. En cada punto, se agregan los niveles del evento o se calcula un promedio hasta alcanzar un «nivel acumulativo» o el valor del índice de ruido. Esta parte del proceso se describe en las secciones 2.7.20 y 2.7.23 a 2.7.25.

En las secciones 2.7.26 a 2.7.28 se resumen las opciones y los requisitos para vincular las curvas de nivel de ruido a los valores del índice de ruido obtenidos para el conjunto de puntos. También se ofrece orientación acerca de la generación de curvas de nivel y del procesamiento posterior.

2.7.3. Concepto de segmentación.

Para una aeronave específica, la base de datos contiene relaciones de ruido-potencia-distancia (NPD). Estas definen, para un vuelo recto uniforme a una velocidad de referencia en condiciones atmosféricas de referencia y en una configuración de vuelo específica, los niveles de los eventos, tanto los máximos como los integrados en el tiempo, directamente debajo de la aeronave⁶ en función de la distancia. A efectos de modelización del ruido, toda la potencia de propulsión significativa se representa mediante un parámetro de potencia relacionado con el ruido; el parámetro que se suele utilizar es el empuje neto corregido. Los niveles de ruido del evento iniciales determinados a partir de la base de datos se ajustan para representar, en primer lugar, las diferencias entre las condiciones atmosféricas reales (es decir, modelizadas) y las de referencia y (en el caso de los niveles de exposición al ruido) la velocidad de la aeronave y, en segundo lugar, para los puntos del receptor que no están directamente debajo de la aeronave, las diferencias entre el ruido irradiado hacia abajo y lateralmente. Esta última diferencia se debe a la directividad lateral (efectos de instalación del motor) y a la atenuación lateral. No obstante, los niveles de ruido del evento ajustados continúan refiriéndose solo al ruido total de la aeronave en vuelo uniforme.

⁶ En realidad, debajo de la aeronave en perpendicular al eje aerodinámico del ala y a la dirección del vuelo; se considera en vertical por debajo de la aeronave en vuelo sin viraje (es decir, sin alabeo).

La segmentación es el proceso mediante el cual el modelo de cálculo de curvas de nivel de ruido recomendado adapta la relación de NPD de la trayectoria infinita y los datos laterales para calcular el ruido que llega a un receptor desde una trayectoria de vuelo no uniforme, es decir, una a lo largo de la cual varía la configuración del vuelo de la aeronave. A los efectos de calcular el nivel de ruido del evento originado por el movimiento de una aeronave, la trayectoria del vuelo se representa mediante un conjunto de segmentos rectilíneos continuos, cada uno de los cuales puede considerarse como una parte finita de una trayectoria infinita para las que se conocen la relación de NPD y los ajustes laterales. El nivel máximo del evento es sencillamente el más alto de los valores de los segmentos individuales. El nivel integrado en el tiempo de ruido total se calcula sumando el ruido recibido desde un número suficiente de segmentos, es decir, los que realizan una contribución significativa al ruido total del evento.

El método para estimar cuándo contribuye el ruido de un segmento finito al nivel del ruido total del evento integrado es puramente empírico. La fracción de la energía F ‒el ruido del segmento expresado como una proporción del ruido de la trayectoria infinita total‒ se describe mediante una expresión relativamente sencilla basada en la directividad longitudinal del ruido de la aeronave y la «vista» del segmento desde el receptor. Una razón por la cual un método empírico sencillo resulta conveniente es que, por norma general, la mayor parte del ruido procede del segmento adyacente que suele estar más próximo ‒el punto de aproximación máxima (CPA) al receptor se encuentra dentro del segmento (y no en ninguno de sus extremos)‒. Esto significa que los cálculos del ruido de segmentos no adyacentes pueden aproximarse cada vez más a medida que se alejan del receptor sin comprometer la precisión significativamente.

2.7.4. Trayectorias del vuelo: Pistas y perfiles.

En el contexto de modelización, una ruta de vuelo (o trayectoria) es una descripción completa del movimiento de la aeronave en espacio y tiempo⁷. Junto con la tracción propulsiva (u otro parámetro de potencia relacionado con el ruido), constituye la información necesaria para calcular el ruido generado. La trayectoria en tierra es la proyección vertical de la trayectoria del vuelo a nivel del terreno. Se combina con el perfil de vuelo vertical para crear una trayectoria de vuelo en 3D. Para la modelización de la segmentación es necesario describir la trayectoria del vuelo de cada movimiento diferente de la aeronave mediante una serie de segmentos rectos contiguos. La forma en que se realiza la segmentación depende de la necesidad de equilibrar la precisión y la eficacia ‒es necesario aproximar lo suficiente la trayectoria del vuelo curvada real al mismo tiempo que se minimizan los límites de cálculo y los requisitos de datos‒. Es necesario definir cada segmento mediante coordenadas geométricas de sus puntos finales y los parámetros de la velocidad asociada y la potencia del motor de la aeronave (de los que depende la emisión de ruido). Las trayectorias de los vuelos y la potencia del motor pueden determinarse de varias formas; la primera de ellas implica a) la síntesis de una serie de pasos procedimentales y b) el análisis de los datos del perfil de vuelo medido.

⁷ El tiempo se contabiliza mediante la velocidad de la aeronave.

Para la síntesis de la trayectoria del vuelo (a) es preciso conocer (o realizar hipótesis de) las trayectorias en tierra y sus dispersiones laterales, los procedimientos de gestión de la velocidad, los flaps y el empuje, la elevación del aeropuerto y la temperatura del viento y del aire. Las ecuaciones para calcular el perfil de vuelo a partir de los parámetros aerodinámicos y de propulsión necesarios se facilitan en el apéndice B. Cada ecuación contiene coeficientes (o constantes) que se basan en datos empíricos para cada tipo de aeronave específico. Las ecuaciones de rendimiento aerodinámico del apéndice B permiten considerar cualquier combinación razonable del procedimiento del vuelo y del peso operacional de la aeronave, incluidas las operaciones de los diferentes pesos brutos de despegue.

El análisis de los datos medidos (b), por ejemplo, a partir de los registros de datos de vuelos, radares u otros equipos de seguimiento de la aeronave, implica «ingeniería inversa», efectivamente una inversión del proceso de síntesis (a). En lugar de calcular los estados de la aeronave y del sistema motopropulsor en los extremos de los segmentos del vuelo mediante la integración de los efectos de las fuerzas de empuje y aerodinámicas que actúan sobre el fuselaje, las fuerzas se calculan mediante la diferenciación de los cambios de altura y velocidad del fuselaje. Los procedimientos para procesar la información de la trayectoria del vuelo se describen en la sección 2.7.12.

En una última aplicación del modelizado del ruido, cada vuelo individual, en teoría, podría representarse de manera independiente; de esta forma, se garantizaría una contabilización precisa de la dispersión espacial de las trayectorias de vuelos, un aspecto que puede resultar muy importante. No obstante, para mantener el tiempo de utilización del ordenador y de preparación de los datos dentro de unos límites razonables, es una práctica habitual representar el alineamiento de la trayectoria del vuelo mediante un número reducido de «subtrayectorias» desplazadas lateralmente. (La dispersión vertical normalmente se representa satisfactoriamente mediante el cálculo de los efectos de las masas variables de las aeronaves en los perfiles verticales).

2.7.5. Rendimiento y ruido de las aeronaves.

La base de datos ANP tratada en el apéndice I abarca la mayoría de los tipos de aeronaves existentes. Si se trata de tipos o variantes de aeronaves cuyos datos no se facilitan actualmente, pueden representarse mediante los datos de otras aeronaves que suelen ser similares.

La base de datos ANP incluye «pasos procedimentales» predeterminados para permitir la creación de perfiles de vuelos al menos para un procedimiento común de salida de reducción de ruidos. Las entradas más recientes de la base de datos abarcan dos procedimientos distintos de salida de reducción de ruidos.

2.7.6. Operaciones del aeropuerto y de las aeronaves.

Los datos específicos según el caso a partir de los cuales se calculan las curvas de nivel de ruido para un escenario particular de aeropuerto comprenden lo siguiente:

Datos generales de los aeropuertos.

‒ El punto de referencia del aeródromo (solo para situar el aeródromo en las coordenadas geográficas apropiadas). El punto de referencia se define como el origen del sistema local de coordenadas cartesianas utilizado en el procedimiento de cálculo.

‒ La altitud de referencia del aeródromo (= altitud del punto de referencia del aeródromo). Se trata de la altitud del plano de tierra nominal con respecto al cual se determinan las curvas de nivel de ruido, en ausencia de correcciones topográficas.

‒ Los parámetros meteorológicos medios en el punto de referencia del aeródromo o próximos a dicho punto (temperatura, humedad relativa, velocidad media del viento y dirección del viento).

Datos de la pista.

Para cada pista:

‒ Designación de la pista.

‒ Punto de referencia de la pista (centro de la pista expresado en coordenadas locales).

‒ Gradiente medio, dirección y longitud de la pista.

‒ Ubicación del punto de partida de rodaje y umbral de aterrizaje⁸.

⁸ Los umbrales desplazados se pueden tener en cuenta mediante la definición de pistas adicionales.

Datos de la trayectoria en tierra.

Las trayectorias en tierra de la aeronave deben describirse mediante una serie de coordenadas en el plano de tierra (horizontal). La fuente de datos de las trayectorias en tierra depende de que los datos de radar pertinentes estén disponibles o no. Si lo están, es necesario establecer una trayectoria principal fiable y las subtrayectorias asociadas adecuadas (dispersas) mediante análisis estadísticos de los datos. En cambio, si no se encuentran disponibles, las trayectorias principales suelen crearse a partir de información procedimental apropiada, por ejemplo, mediante la utilización de procedimientos de salida normalizados por instrumentos que constan en las publicaciones de información aeronáutica. Esta descripción convencional incluye la siguiente información:

‒ Designación de la pista desde la que se origina la trayectoria.

‒ Descripción del origen de la trayectoria (punto de partida de rodaje y umbral de aterrizaje).

‒ Longitud de los segmentos (para giros, radios y cambios de dirección).

Esta información constituye el mínimo necesario para definir la trayectoria principal. No obstante, los niveles medios de ruido calculados sobre el supuesto de que la aeronave sigue estrictamente las rutas nominales pueden ser responsables de errores localizados de varios decibelios. Por tanto, debe representarse la dispersión lateral, y se precisa la siguiente información adicional:

‒ Anchura de la banda de dispersión (u otra estadística de dispersión) en cada extremo del segmento.

‒ Número de subtrayectorias.

‒ Distribución de movimientos perpendiculares a la trayectoria principal.

Datos del tráfico aéreo.

Los datos del tráfico aéreo son:

‒ el período de tiempo cubierto por los datos, y

‒ el número de movimientos (llegadas o salidas) de cada tipo de aeronave en cada trayectoria de vuelo, subdividido por 1) el período del día, según proceda, apropiado a los descriptores de ruido específicos, 2) para salidas, pesos operativos o longitudes de las etapas, y 3) procedimientos operativos, si procede.

La mayoría de los descriptores de ruido requieren que los eventos (es decir, los movimientos de la aeronave) se definan como valores diarios medios durante los períodos específicos del día (por ejemplo, el día, la tarde y la noche); véanse las secciones 2.7.23 a 2.7.25.

Datos topográficos.

El terreno alrededor de la mayoría de los aeropuertos es relativamente llano. No obstante, no siempre es el caso, y algunas veces puede resultar necesario tener en cuenta las variaciones de la elevación del terreno en relación a la elevación de referencia del aeropuerto. El efecto de la elevación del terreno puede resultar particularmente importante en las proximidades de las rutas de aproximación, donde la aeronave opera a altitudes relativamente bajas.

Los datos de la elevación del terreno suelen facilitarse como un conjunto de coordenadas (x,y,z) para una malla rectangular de un paso de malla determinado. No obstante, es probable que los parámetros de la malla de elevación difieran de los de la malla utilizada para calcular el ruido. En su caso, se puede utilizar una interpolación lineal para calcular las coordenadas z apropiadas a la malla de cálculo.

El análisis integral de los efectos del terreno con desniveles marcados en la propagación sonora es complejo y está fuera del alcance de este método. La irregularidad moderada se puede tener en cuenta suponiendo un terreno «pseudonivel»; es decir, simplemente aumentando o reduciendo el nivel del plano de tierra a la elevación del terreno local (en relación con el plano de tierra de referencia) en cada punto del receptor (véase la sección 2.7.4).

Condiciones de referencia.

Los datos internacionales de rendimiento y ruido de la aeronave (ANP) se normalizan para condiciones de referencia estándar que se usan ampliamente para estudios de ruido en aeropuertos (véase el apéndice D).

Condiciones de referencia para los datos de NPD.

1) Presión atmosférica: 101,325 kPa (1 013,25 mb).

2) Absorción atmosférica: Parámetros de atenuación enumerados en el cuadro D-1 del apéndice D.

3) Precipitaciones: Ninguna.

4) Velocidad del viento: Menos de 8 m/s (15 nudos).

5) Velocidad respecto a tierra: 160 nudos.

6) Terreno local: Superficie llana y suave sin estructuras grandes ni otros objetos reflectantes dentro de un radio de varios kilómetros de las trayectorias en tierra de las aeronaves.

Las medidas estandarizadas del sonido de la aeronave se realizan a 1,2 m por encima de la superficie del terreno. No obstante, no es necesario prestar especial atención a esto ya que, a efectos de modelización, se puede asumir que los niveles de los eventos son relativamente insensibles a la altura del receptor⁹.

⁹ A veces se piden niveles calculados a 4 m o más. La comparación de las medidas a 1,2 m y a 10 m y el cálculo teórico de los efectos de suelo revelan que las variaciones del nivel de exposición al ruido con ponderación A son relativamente insensibles a la altura del receptor. Las variaciones suelen ser inferiores a un decibelio, salvo si el ángulo máximo de la incidencia de sonido es inferior a 10° y si el espectro ponderado A en el receptor tiene su nivel máximo dentro del rango comprendido entre 200 Hz y 500 Hz. Dicha variabilidad dominada por una baja frecuencia puede producirse, por ejemplo, a largas distancias para motores con una relación de derivación baja y para motores de hélice con tonos de frecuencia baja discretos.

Las comparaciones entre los niveles de ruido del aeropuerto calculados y medidos indican que se puede suponer que los datos de NPD son aplicables cuando las condiciones medias de la superficie cercana presentan las siguientes características:

‒ Temperatura del aire inferior a 30 °C.

‒ Producto de la temperatura del aire (°C), y humedad relativa, (porcentaje) superior a 500.

‒ Velocidad del viento inferior a 8 metros por segundo (15 nudos).

Se estima que estas características engloban las condiciones encontradas en la mayoría de los principales aeropuertos del mundo. En el apéndice D se ofrece un método para convertir los datos de NPD en condiciones medias locales que están fuera de este rango, pero en casos extremos, se sugiere consultar a los fabricantes correspondientes de la aeronave.

Condiciones de referencia para los datos del motor y la aerodinámica de la aeronave.

1) Elevación de la pista: Nivel medio del mar.

2) Temperatura del aire: 15 °C.

3) Peso bruto en despegue: Como se define en función de la longitud de la etapa en la base de datos de ANP.

4) Peso bruto en aterrizaje: 90 % del peso bruto máximo en aterrizaje.

5) Motores con empuje: Todos.

A pesar de que los datos del motor y aerodinámicos de ANP se basan en estas condiciones, se pueden usar como tabulados estos para elevaciones de la pista distintas de las de referencia y temperaturas promedio medias del aire en los Estados de la CEAC sin afectar significativamente a la precisión de las curvas de los niveles medios de ruido acumulados. (Véase el apéndice B).

La base de datos de ANP tabula los datos aerodinámicos para los pesos brutos de despegue y aterrizaje indicados en los puntos 3 y 4 anteriores. A pesar de que, para cálculos del ruido total acumulado, los datos aerodinámicos deben ajustarse para otros pesos brutos, el cálculo de los perfiles del vuelo en despegue y ascenso, usando los procedimientos descritos en el apéndice B, debe basarse en los pesos brutos del despegue operativo apropiados.

2.7.7. Descripción de la trayectoria del vuelo.

El modelo de ruido requiere que cada movimiento diferente de la aeronave se describa mediante su trayectoria de vuelo tridimensional y la potencia variable del motor y su velocidad. Como norma, un movimiento modelizado representa un subconjunto del tráfico total del aeropuerto, por ejemplo, un número de movimientos idénticos (asumidos como tales), con el mismo tipo de aeronave, peso y procedimiento operativo, sobre una única trayectoria en tierra. Dicha trayectoria puede ser una de varias «subtrayectorias» dispersas utilizadas para modelizar lo que realmente es una dispersión de trayectorias siguiendo una ruta designada. Las dispersiones de la trayectoria en tierra, los perfiles verticales y los parámetros operativos de la aeronave se determinan a partir de los datos del escenario de entrada, junto con los datos de la aeronave extraídos de la base de datos de ANP.

Los datos de ruido-potencia-distancia (en la base de datos de ANP) definen el ruido procedente de una aeronave que recorren trayectorias de vuelo horizontales idealizadas de longitud infinita a una potencia y velocidad constantes. Para adaptar estos datos a las trayectorias de vuelo del área terminal caracterizadas por cambios frecuentes de potencia y velocidad, cada trayectoria se divide en segmentos rectilíneos finitos; las contribuciones de ruido de cada uno de ellos se suman posteriormente en la posición del observador.

2.7.8. Relaciones entre la trayectoria del vuelo y la configuración del vuelo.

La trayectoria del vuelo tridimensional del movimiento de una aeronave determina los aspectos geométricos de la radiación y la propagación del sonido entre la aeronave y el observador. Con un peso particular y en condiciones atmosféricas particulares, la trayectoria del vuelo se rige completamente mediante la secuencia de potencia, flaps y cambios de altitud aplicados por el piloto (o sistema de gestión automática del vuelo), a fin de seguir rutas y mantener las alturas y velocidades especificadas por el control de tránsito aéreo (CTA), en virtud de los procedimientos operativos estándar del operador de aeronaves. Estas instrucciones y acciones dividen la trayectoria del vuelo en distintas fases que conforman los segmentos naturales. En el plano horizontal, implican tramos rectos, especificados como una distancia hasta el próximo giro y los próximos giros, definida por el radio y el cambio de rumbo. En el plano vertical, los segmentos se definen mediante el tiempo o la distancia considerados para conseguir los cambios necesarios de velocidad de avance o altura en los ajustes de flaps y potencia especificados. A menudo, a las coordenadas verticales correspondientes las denomina puntos de perfil.

Para la modelización del ruido, se genera información sobre la trayectoria del vuelo mediante la síntesis de un conjunto de pasos procedimentales (es decir, los que sigue el piloto) o mediante el análisis de los datos de los radares ‒medidas físicas de las trayectorias de vuelo reales en el aire‒. Con independencia del método que se utilice, las formas horizontales y verticales de la trayectoria de vuelo se reducen a formas segmentadas. Su forma horizontal (es decir, su proyección bidireccional sobre el suelo) es la trayectoria en tierra definida por el itinerario entrante y saliente. Su forma vertical, obtenida mediante los puntos de perfil, y los parámetros de vuelo asociados de velocidad, ángulo de alabeo y reglaje de la potencia, en conjunto definen el perfil del vuelo que depende el procedimiento del vuelo que suele prescribir el fabricante de la aeronave o el operador. La trayectoria del vuelo se crea mediante la fusión del perfil del vuelo bidimensional con la trayectoria en tierra bidimensional para formar una secuencia de segmentos de la trayectoria del vuelo tridimensional.

Cabe recordar que, para un conjunto de pasos procedimentales determinado, el perfil depende de la trayectoria en tierra; por ejemplo, con el mismo empuje y a la misma velocidad, la velocidad de ascenso en inferior, a su vez, que el vuelo en línea recta. Aunque en este documento se explica cómo tener en cuenta esta dependencia, hay que reconocer que ello supondría, por norma general, una excesiva sobrecarga de cálculo y los usuarios pueden preferir asumir que, a efectos de modelización del ruido, el perfil del vuelo y la trayectoria en tierra pueden tratarse como entidades independientes, es decir que el perfil de ascenso no se ve afectado por ningún giro. No obstante, es importante determinar los cambios del ángulo de alabeo que los giros necesitan, porque esto influye significativamente en la direccionalidad de la emisión de sonido.

El ruido recibido desde un segmento de la trayectoria del vuelo depende de la geometría del segmento en relación con el observador y la configuración del vuelo de la aeronave. Pero estos parámetros están interrelacionados; de hecho, un cambio en uno causa un cambio en el otro, y es necesario garantizar que, en todos los puntos de la trayectoria, la configuración de la aeronave está en consonancia con su movimiento a lo largo de la trayectoria.

En la síntesis de la trayectoria de un vuelo, es decir, al crear la trayectoria de un vuelo a partir de un conjunto de «pasos procedimentales» que describen las selecciones que el piloto realiza de la potencia del motor, el ángulo de los flaps y la velocidad vertical o de aceleración, lo que hay que calcular es el movimiento. En el análisis de la trayectoria de un vuelo, se da el caso contrario: es necesario calcular la potencia del motor a partir del movimiento observado de la aeronave, según los datos del radar o, en algunas ocasiones, en estudios especiales, a partir de los datos del registrador del vuelo de la aeronave (aunque en el último caso, la potencia del motor suele formar parte de los datos). En ambos casos, las coordenadas y los parámetros del vuelo en todos los puntos finales del segmento deben introducirse en el cálculo del ruido.

En el apéndice B se presentan las ecuaciones que relacionan las fuerzas que actúan sobre una aeronave y su movimiento y se explica cómo se resuelven para definir las propiedades de los segmentos que conforman las trayectorias de los vuelos. Los diferentes tipos de segmentos (y las secciones del apéndice B en que se tratan) son el empuje en tierra al despegar (B5), el ascenso a una velocidad constante (B6), la aceleración en ascenso y la retracción de los flaps (B8), la aceleración en ascenso después de la retracción de los flaps (B9), el descenso y la deceleración (B10) y aproximación final de aterrizaje (B11).

Inevitablemente, la modelización práctica implica grados variables de simplificación ‒el requisito para ello depende de la naturaleza de la aplicación del método, de la importancia de los resultados y de los recursos disponibles‒. Un supuesto simplificado general, incluso en las aplicaciones más elaboradas, es que, al calcular la dispersión de la trayectoria del vuelo, los perfiles y las configuraciones del vuelo en todas las subtrayectorias son los mismos que los de la trayectoria principal. Como se deben utilizar al menos 6 subtrayectorias (véase la sección 2.7.11), esto reduce los cálculos masivos que implican una penalización sumamente pequeña en términos de confianza.

2.7.9. Fuentes de los datos de las trayectorias de vuelos.

Datos de radares.

Aunque los registradores de datos de vuelos de aeronaves pueden generar datos de muy alta calidad, es difícil obtenerlos a efectos de modelización del ruido, por lo que los datos de los radares pueden considerarse como la fuente de información de más fácil acceso sobre las trayectorias de vuelo reales en el aire en los aeropuertos¹⁰. Habida cuenta de que suelen encontrarse disponibles en los sistemas de supervisión de la trayectoria del vuelo y del ruido en los aeropuertos, actualmente se usan cada vez más a efectos de modelización del ruido.

¹⁰ Los registradores de datos de vuelos de aeronaves ofrecen datos de operación integrales. No obstante, no son de fácil acceso y su disponibilidad resulta costosa; por tanto, su uso a efectos de modelización del ruido suele restringirse a estudios para el desarrollo de modelos y proyectos especiales.

El radar secundario de vigilancia presenta la trayectoria de vuelo de una aeronave como una secuencia de coordenadas de posición a intervalos iguales al período de rotación del escáner de radar, normalmente en torno a 4 segundos. La posición de la aeronave con respecto al suelo se determina en coordenadas polares ‒distancia y acimut‒ a partir de las señales de retorno de radar reflejadas (aunque el sistema de control suele transformarlas en coordenadas cartesianas); su altura¹¹ se mide por medio del altímetro propio del avión y se transmite al ordenador de control del tráfico aéreo mediante un transpondedor de radar. No obstante, los errores de posición inherentes por la interferencia de radiofrecuencias y la resolución de datos limitados resultan importantes (a pesar de que no tiene ninguna consecuencia para los fines previstos de control del tráfico aéreo). Por lo tanto, si es necesario conocer la trayectoria del vuelo del movimiento de una aeronave específica, es preciso suavizar los datos mediante una técnica apropiada para el ajuste de curvas. No obstante, a efectos de modelización del ruido, suele ser necesario realizar una descripción estadística de la dispersión de las trayectorias de los vuelos; por ejemplo, para todos los movimientos de una ruta o solo para los de un tipo de aeronave específica. En este ámbito, los errores de mediciones asociados con las estadísticas correspondientes pueden reducirse hasta ser irrelevantes mediante procesos de determinación del promedio.

¹¹ Por lo general, esto se mide como altitud sobre MSL (es decir, en relación a 1.013 mB) y se corrige con respecto a la elevación del aeropuerto mediante el sistema de supervisión del aeropuerto.

Etapas del procedimiento.

En muchos casos, no es posible modelizar las trayectorias de los vuelos en función de los datos del radar, porque no se encuentran disponibles los recursos necesarios, o bien porque se trata de un futuro escenario para el que no se encuentran disponibles los datos de radar que resultan pertinentes.

A falta de datos de radar, o cuando su uso resulta inapropiado, es necesario calcular las trayectorias de los vuelos conforme al material guía operativo, por ejemplo las instrucciones que se dan al personal del vuelo en las publicaciones de información aeronáutica (AIP) y en manuales de funcionamiento de la aeronave, lo que aquí se denomina como etapas del procedimiento. Cuando proceda, las autoridades de control del tráfico aéreo y los operadores de la aeronave proporcionarán asesoramiento acerca de cómo interpretar dicho material.

2.7.10. Sistemas de coordenadas.

Sistema de coordenadas local.

El sistema de coordenadas locales (x,y,z) es el cartesiano y tiene su origen (0,0,0) en el punto de referencia del aeródromo (X_ARP,Y_ARP,Z_ARP), donde Z_ARP es la altitud de referencia del aeropuerto y z = 0 define el plano del terreno nominal sobre el cual suelen calcularse las curvas de nivel de ruido. El rumbo de la aeronave ξ en el plano xy se mide en el sentido de las agujas del reloj a partir del Norte magnético (véase la figura 2.7.b). Todas las ubicaciones del observador, la malla de cálculo básica y los puntos se expresan en coordenadas locales¹².

¹² Normalmente, los ejes de las coordenadas locales son paralelos al eje del mapa en el que se dibujan las isófonas. No obstante, a veces resulta útil elegir el eje x paralelo a una pista, a fin de obtener curvas simétricas sin utilizar una malla de cálculo fina (véanse las secciones 2.7.26 a 2.7.28).

Figura 2.7.b

Sistema de coordenadas locales (x,y,z) y coordenadas fijas de la trayectoria en tierra

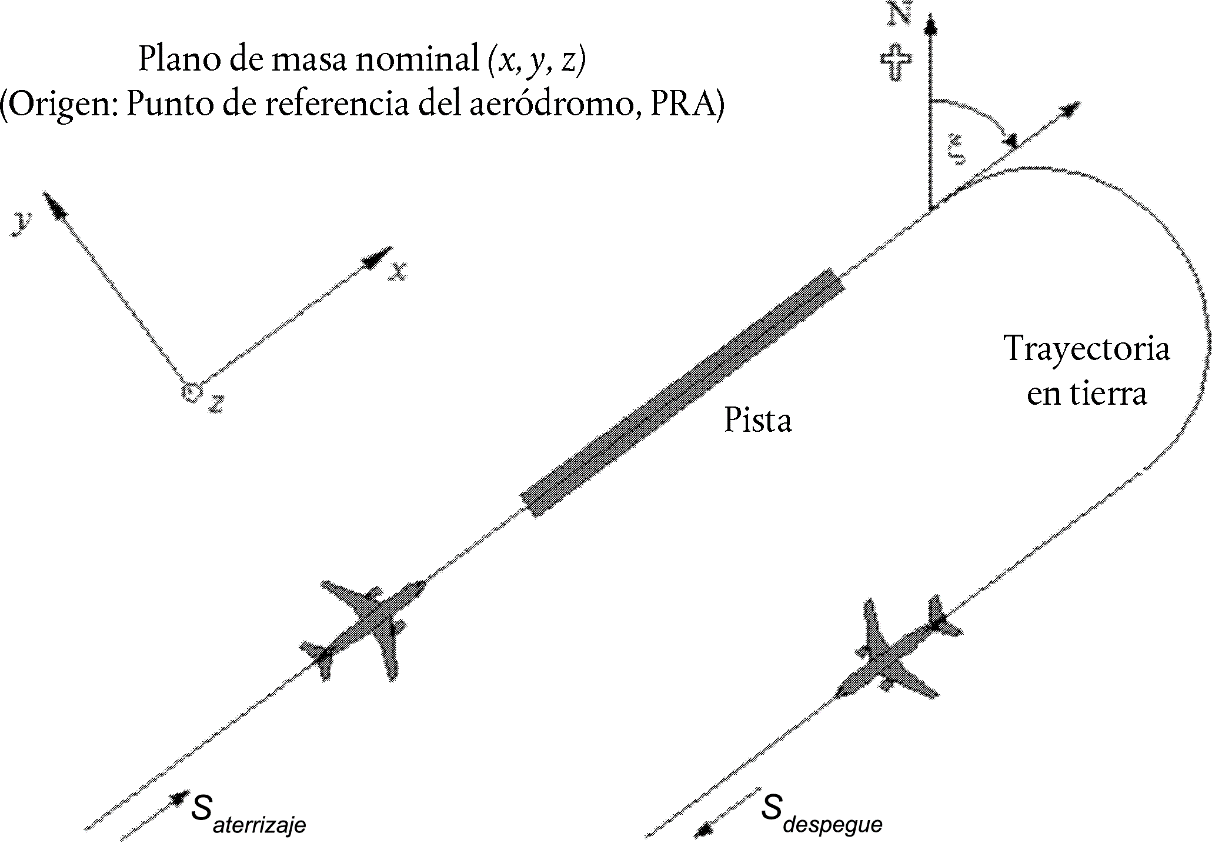
Sistema de coordenadas fijas de la trayectoria en tierra.

Esta coordenada es específica de cada trayectoria en tierra y representa la distancia s medida a lo largo de la trayectoria en la dirección del vuelo. En las trayectorias de despegue, S se mide desde el inicio de la rodadura y, en el caso de las trayectorias de aterrizaje, desde el umbral de aterrizaje. Por tanto, S resulta negativo en las siguientes zonas:

‒ detrás del punto de partida de rodaje en las salidas;

‒ antes de cruzar el umbral de aterrizaje en pista para las llegadas.

Los parámetros operativos del vuelo, tales como la altura, la velocidad y el reglaje de la potencia, se expresan en fruición de s.

Sistema de coordenadas del avión.

El sistema de coordenadas cartesianas fijas del avión (x',y',z') tiene su origen en la ubicación real del avión. El sistema axial se define mediante el ángulo de subida γ, la dirección del vuelo ξ y el ángulo de alabeo ε (véase la figura 2.7.c).

Figura 2.7.c

Sistema de coordenadas fijas del avión (x', y', z')

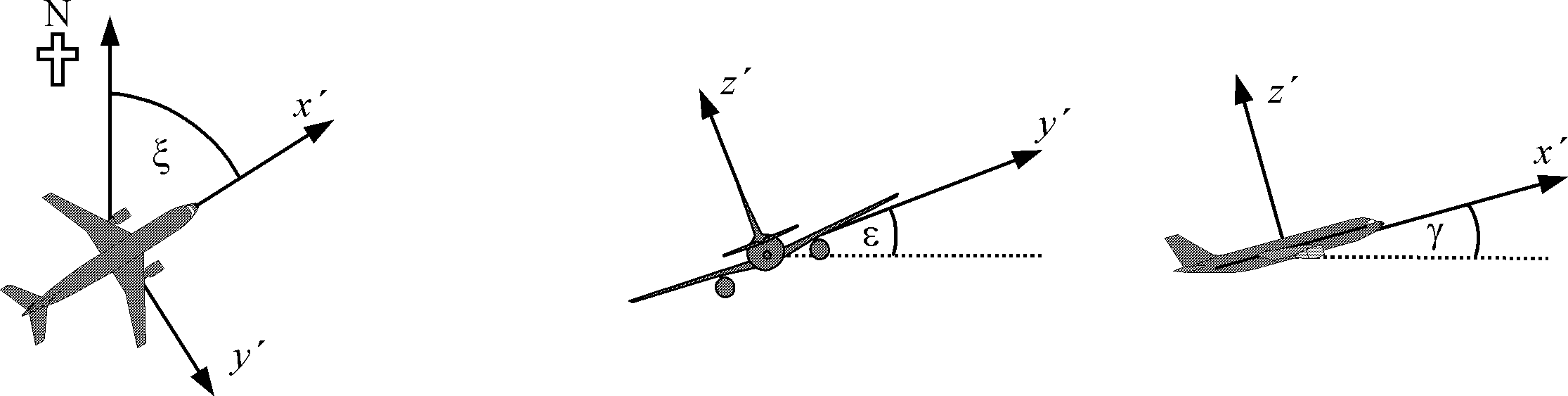
Consideración de la topografía.

En los casos en que es necesario tener en cuenta la topografía (véase la sección 2.7.6), es necesario reemplazar la coordenada de la altura del avión z por z' = z ‒ z_o (donde z_o la coordenada z es la ubicación del observador O) al calcular la distancia de propagación d. La geometría entre el avión y el observador se ilustra en la figura 2.7.d. Para consultar las definiciones de d y ℓ, véanse las secciones 2.7.14 a 2.7.19¹³.

¹³ En terrenos desnivelados puede ser posible que el observador se sitúe por encima de la aeronave. En este caso, para calcular la propagación sonora, se considera z’ (y el correspondiente ángulo de elevación β ‒ ver Capítulo 4) igual a cero.

Figura 2.7.d

Elevación del terreno a la (izquierda) y en el lateral (derecho) de la trayectoria en tierra

(El plano de tierra nominal z = 0 pasa a través del punto de referencia del aeródromo. O es la ubicación del observador)

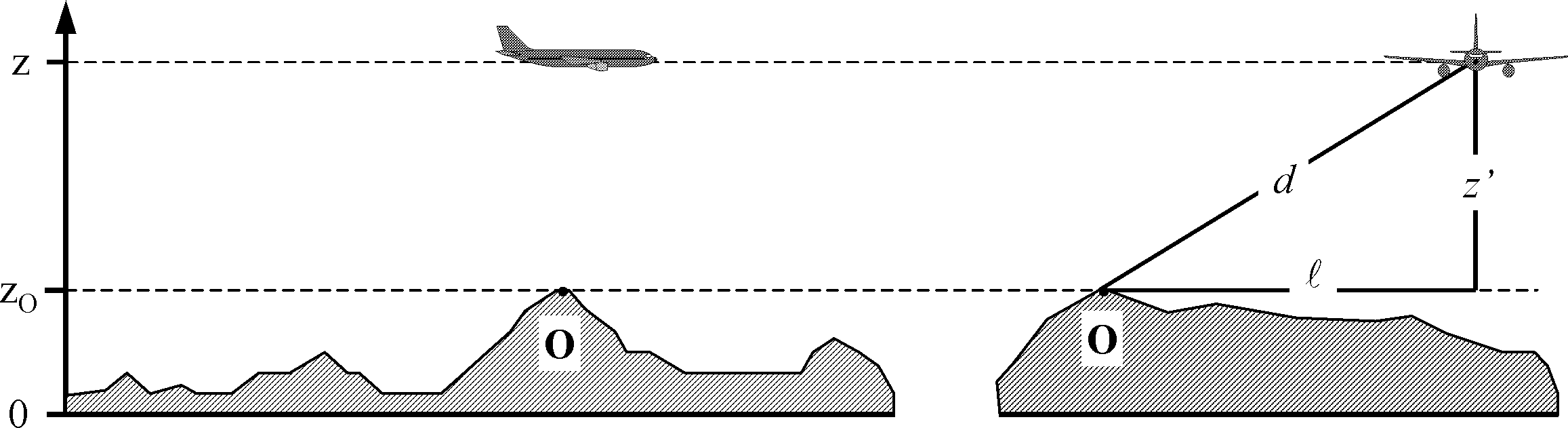
2.7.11. Trayectorias en tierra.

Trayectorias principales.

La trayectoria principal define el centro de la banda de dispersión de las trayectorias que sigue el avión con una ruta. A efectos de modelización del ruido del avión, se define i) mediante datos operativos prescriptivos, como las instrucciones que se dan a los pilotos en las publicaciones de información aeronáutica o ii) mediante análisis estadísticos de los datos de radar, tal como se explica en la sección 2.7.9, cuando se encuentren disponibles y resulten convenientes para satisfacer las necesidades del estudio de modelización. Crear la trayectoria a partir de instrucciones operativas suele ser una tarea bastante sencilla, ya que estas prescriben una secuencia de tramos rectos ‒definidos por la longitud y el rumbo‒ o arcos circulares definidos por la velocidad de viraje y el cambio de rumbo; véase la figura 2.7.e para consultar una ilustración.

Figura 2.7.e

Geometría de la trayectoria en tierra en términos de virajes y segmentos rectos

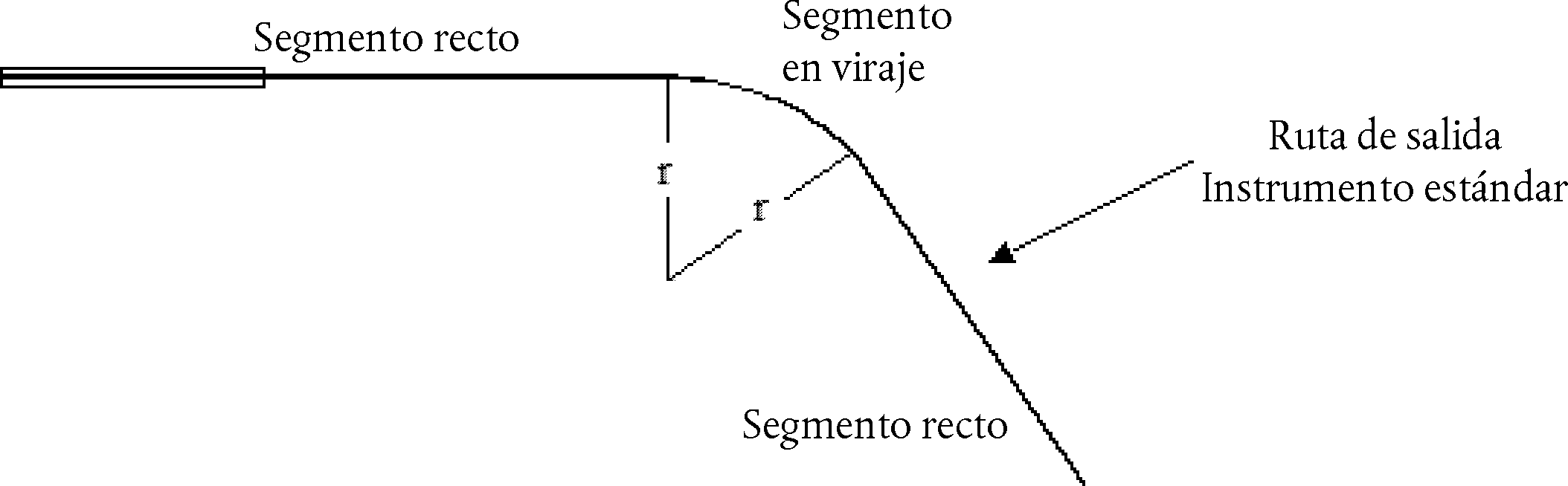
Adecuar la trayectoria principal a los datos de radar es una tarea más compleja, en primer lugar porque se hacen virajes reales a una velocidad variable y, en segundo lugar, porque su línea se oscurece por la dispersión de los datos. Como bien se ha explicado, aún no se han desarrollado procedimientos formalizados y es una práctica habitual asociar segmentos, ya sean rectos o curvados, con las posiciones medias calculadas a partir de los cortes transversales de las líneas de seguimiento por radar a intervalos a lo largo de la ruta. Es posible que los algoritmos informáticos necesarios para ejecutar esta tarea se desarrollen en un futuro, pero, por el momento, compete al modelista decidir cuál es la mejor manera de utilizar los datos disponibles. Un factor importante es que la velocidad del avión y el radio de viraje indican el ángulo de alabeo y, como se observará en la sección 2.7.19, las asimetrías de la radiación sonora en torno a la trayectoria del vuelo influyen en el ruido en tierra, así como la posición de la trayectoria del vuelo.

En teoría, la transición perfecta desde el vuelo recto al viraje de radio fijo precisaría de una aplicación instantánea del ángulo de alabeo ε, que físicamente resulta imposible. En realidad, el ángulo de alabeo tarda un tiempo determinado en alcanzar el valor requerido para mantener una velocidad específica y el radio de viraje r, durante el cual el radio de viraje se ajusta de infinito a r. A efectos de modelización, puede ignorarse la transición del radio y suponerse que el ángulo de alabeo aumenta constantemente desde cero (u otro valor inicial) hasta ε al inicio del viraje y ser el próximo valor de ε al final del viraje¹⁴.

¹⁴ Compete al usuario decidir cuál es la mejor manera de aplicar esta cuestión, ya que ello dependerá de la forma en que se definan los radios de viraje. Cuando el punto de partida es una secuencia de tramos circulares o rectos, una opción relativamente sencilla es insertar los segmentos de transición del ángulo de alabeo al inicio del viraje y al final, donde el avión rueda a una velocidad constante (por ejemplo, expresada en °/m o °/s).

Dispersión de la trayectoria.

Cuando sea posible, las definiciones de la dispersión lateral y de las subtrayectorias representativas se basarán en experiencias pasadas pertinentes del aeropuerto objeto de estudio; normalmente, a través del análisis de las muestras de datos de radar. El primer paso consiste en agrupar los datos por ruta. Las vías de salida se caracterizan por una dispersión lateral sustancial que debe tenerse en cuenta para realizar una modelización precisa. Las rutas de llegada se unen en una banda muy estrecha sobre la ruta de aproximación final, y suele ser suficiente representar todas las llegadas mediante una única trayectoria. No obstante, si las dispersiones en el aterrizaje son amplias, es posible que sea preciso representarlas mediante subtrayectorias de la misma forma que las rutas de salida.

Es una práctica común tratar los datos (información) para una única ruta como una muestra de una única población (estadística); es decir, realizar la representación mediante una trayectoria principal y un conjunto de subtrayectorias dispersas. No obstante, si la inspección indica que los datos de las diferentes categorías de aviones u operaciones difieren significativamente (por ejemplo, en caso de que un avión grande y pequeño tenga radios de viraje bastante diferentes), sería conveniente realizar otra subdivisión de los datos en diferentes bandas de dispersión. Para cada banda, las dispersiones de la trayectoria lateral se determinan en función de la distancia a partir del origen; entonces los movimientos se distribuyen entre una trayectoria principal y un número apropiado de subtrayectorias dispersas en función de las estadísticas de distribución.

Habida cuenta de que suele ser conveniente ignorar los efectos de la dispersión de la trayectoria, ante la ausencia de datos de bandas de dispersión medidos, debe definirse una dispersión lateral a la trayectoria principal y perpendicular a ella mediante una función de distribución convencional. Los valores calculados de los índices de ruido no son particularmente sensibles a la forma precisa de la distribución lateral: la distribución normal (de Gauss) ofrece una descripción adecuada de bandas de dispersión medidas por radar.

Normalmente se usa una aproximación discreta de siete puntos (es decir, que representa la dispersión lateral mediante seis subtrayectorias con la misma separación alrededor de la trayectoria principal). La separación de las subtrayectorias depende de la desviación estándar de la función de dispersión lateral.

En el caso de las trayectorias con una distribución normal y una desviación estándar S, el 98,8 % de las trayectorias se encuentran dentro de un corredor con límites ubicado a ± 2,5×S. En el cuadro 2.7.a se indica la separación de las seis subtrayectorias y el porcentaje de los movimientos totales asignado a cada una. En el apéndice C se ofrecen los valores para los otros números de subtrayectorias.

Cuadro 2.7.a

Porcentajes de movimientos para una función de distribución normal con una desviación estándar S para siete subtrayectorias (la trayectoria principal es la subtrayectoria 1)

Número de subtrayectoria	Ubicación de la subtrayectoria	Porcentaje de movimientos en la subtrayectoria
7	– 2,14 × S	3 %
5	– 1,43 × S	11 %
3	– 0,71 × S	22 %
1	0	28 %
2	0,71 × S	22 %
4	1,43 × S	11 %
6	2,14 × S	3 %

La desviación estándar S es una función de la coordenada s a lo largo de la trayectoria principal. Se puede especificar ‒junto con la descripción de la trayectoria principal‒ en la ficha de datos de la trayectoria del vuelo que se encuentra en el apéndice A3. Ante la ausencia de los indicadores de la desviación normal ‒por ejemplo, a partir de los datos de radar que describen trayectorias de vuelo comparables‒, se recomiendan los valores siguientes:

Para trayectorias que implican virajes de menos de 45 grados:

(2.7.1)

Para trayectorias que implican virajes de más de 45 grados:

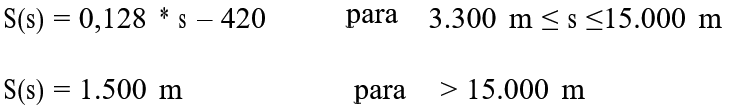
(2.7.2)

Por cuestiones prácticas, se asume el valor 0 para S(s) entre el punto de partida de rodaje y s = 2.700 m o s = 3.300 m, en función de la cantidad de virajes. Las rutas que comprenden más de un viraje deben tratarse en función de la ecuación (2.7.2). Para los aterrizajes, puede obviarse la dispersión lateral dentro de los 6 000 m de la toma de contacto.

2.7.12. Perfiles de vuelos.

El perfil del vuelo es una descripción del movimiento del avión en el plano vertical por encima de la trayectoria en tierra, en términos de su posición, velocidad, ángulo de alabeo y reglaje de la potencia del motor. Una de las tareas más importantes que tiene que realizar el usuario del modelo es la definición de perfiles de vuelo que satisfagan correctamente los requisitos de la aplicación de la modelización, de una manera eficiente y sin emplear mucho tiempo ni demasiados recursos. Naturalmente, para conseguir una alta precisión, los perfiles tienen que reflejar fielmente las operaciones del avión que pretenden representar. Para ello se precisa información fiable sobre las condiciones atmosféricas, los tipos de avión y las versiones, pesos operativos (o de operación) y procedimientos operativos (o de operación) ‒las variaciones de empuje y configuración de los flaps y compensaciones entre cambios de altitud y velocidad‒, calculando el promedio de todos los factores con respecto a los períodos de tiempo pertinentes. A menudo, no se encuentra disponible información detallada, pero esto no plantea necesariamente un obstáculo; incluso aunque sí se encuentren disponibles, el modelista tiene que encontrar el equilibrio entre la precisión y el nivel de detalle de la información de entrada que necesita y utiliza para obtener las curvas de nivel de ruido.

La síntesis de los perfiles de vuelos de las «etapas del procedimiento» obtenidos de la base de datos de ANP o que proporcionan los operadores del avión se describe en la sección 2.7.13 y en el apéndice B. Dicho proceso, que suele ser el único recurso disponible para el modelista cuando no hay datos de radar disponibles, ofrece la geometría de la trayectoria del vuelo y las variaciones de empuje y velocidad asociados. Normalmente puede asumirse que todos los aviones (iguales) de una determinada banda de dispersión, independientemente de que estén asignados a la trayectoria principal o a subtrayectorias dispersas, siguen el perfil de la trayectoria principal.

Más allá de la base de datos de ANP, que ofrece información predeterminada sobre las etapas del procedimiento, los operadores del avión constituyen la mejor fuente de información fiable, es decir, los procedimientos que utilizan y los típicos pesos volados. Para los vuelos individuales, la fuente «tipo de referencia» es el registrador de los datos del vuelo del avión (FDR) del que se puede obtener toda la información pertinente. Pero incluso aunque tales datos se encuentren disponibles, la tarea de preprocesamiento resulta formidable. Por tanto, y teniendo en cuenta las economías de modelización necesarias, la solución práctica común es hacer hipótesis contrastadas acerca de pesos medios y los procedimientos operativos.

Es necesario tener precaución antes de adoptar las etapas predeterminadas del procedimiento establecidas en la base de datos de ANP (que se asumen habitualmente cuando los procedimientos reales no se conocen). Se trata de procedimientos normalizados ampliamente observados, que los operadores pueden o no utilizar en casos particulares. Un factor importante es la definición del empuje del reactor en el despegue (y a veces en el ascenso), que puede depender en cierta medida de circunstancias imperantes. En particular, es una práctica común reducir los niveles de empuje durante el despegue (a partir del máximo disponible), a fin de ampliar la vida útil del motor. En el apéndice B se ofrece orientación sobre la representación de la práctica habitual; por lo general, esto generará curvas de nivel de ruido más realistas que la hipótesis de un empuje total. No obstante, si, por ejemplo, las pistas son cortas o las temperaturas medias del aire son altas, el empuje total podría constituir una hipótesis más realista.

Al modelizar escenarios reales, se puede conseguir mayor precisión con los datos de radar, a fin de complementar o reemplazar esta información nominal. Los perfiles de vuelos pueden determinarse a partir de los datos de radar de una forma similar a la de las trayectorias principales laterales ‒pero solo después de separar el tráfico por tipo y variante de avión y, a veces, por peso o longitud de la etapa (pero no en función de la dispersión)‒ a fin de obtener, para cada subgrupo, un perfil medio de altura y velocidad con respecto a la distancia de terreno recorrida. Una vez más, al realizar la combinación con las trayectorias en tierra posteriormente, este perfil único suele asignarse a la trayectoria principal y a las subtrayectorias por igual.

Conociendo el peso del avión, la variación de la velocidad y e l empuje se puede calcular a través de un procedimiento paso a paso basado en ecuaciones de movimiento. Antes de ello, resulta útil procesar previamente los datos a fin de minimizar los efectos de los errores de radar que pueden hacer que los cálculos de aceleración resulten poco fiables. El primer paso en cada caso consiste en redefinir el perfil conectando los segmentos rectilíneos para representar las etapas pertinentes del vuelo, de tal manera que cada segmento se clasifique correctamente, es decir, como un desplazamiento en tierra firme, ascenso o descenso a velocidad constante, reducción de empuje o aceleración o desaceleración con o sin cambio de la posición de los flaps. El peso del avión y las condiciones atmosféricas también constituyen información necesaria.

En la sección 2.7.11 se pone de manifiesto que se debe considerar un método específico para tener en cuenta la dispersión lateral de las rutas nominales o trayectorias principales. Las muestras de datos de radar se caracterizan por dispersiones similares de trayectorias de vuelos en el plano vertical. No obstante, no es una práctica habitual modelizar la dispersión vertical como una variable independiente; surge principalmente por las diferencias entre el peso del avión y los procedimientos operativos que se tienen en cuenta al preprocesar los datos de entrada de tráfico.

2.7.13. Construcción de segmentos de trayectorias de vuelo.

Cada trayectoria de vuelo tiene que definirse mediante un conjunto de coordenadas de segmentos (nodos) y parámetros de vuelo. El origen se tiene en cuenta para determinar las coordenadas de los segmentos de la trayectoria en tierra. A continuación, se calcula el perfil del vuelo, recordando que, para un conjunto de etapas del procedimiento de vuelo determinado, el perfil depende de la trayectoria en tierra; por ejemplo, con el mismo empuje y a la misma velocidad, la velocidad de ascenso en inferior, a su vez, que la del vuelo en línea recta. Por último, los segmentos de la trayectoria del vuelo tridimensional se construyen mediante la combinación del perfil bidimensional del vuelo y la trayectoria en tierra tridimensional¹⁵.

¹⁵ Para este fin, la longitud total de la trayectoria en tierra siempre debe exceder la del perfil del vuelo. Esto puede conseguirse, si resulta necesario, con la incorporación de segmentos rectos de longitud adecuada al último segmento de la trayectoria en tierra.

Trayectoria en tierra.

Una trayectoria en tierra, ya sea una trayectoria principal o una subtrayectoria dispersa, se define mediante una serie de coordenadas (x,y) en el plano de tierra (por ejemplo, a partir de la información de radar) o mediante una secuencia de comandos vectoriales que describen los segmentos rectos y los arcos circulares (virajes de radio definido r y cambio de rumbo Δξ).

Para la modelización de la segmentación, un arco se representa mediante una secuencia de segmentos rectos colocados en los subarcos. Aunque no aparecen explícitamente en los segmentos de la trayectoria en tierra, el alabeo del avión durante los virajes influye en su definición. En el apéndice B4 se explica cómo calcular los ángulos de alabeo durante un viraje uniforme pero, evidentemente, no se aplican realmente ni se eliminan al instante. No se prescribe cómo gestionar las transiciones entre los vuelos rectos y en viraje, o bien entre un viraje y uno inmediatamente secuencial. Por norma general, los detalles, que competen al usuario (véase la sección 2.7.11), pueden tener un efecto insignificante en las curvas de nivel de ruido finales; el requisito consiste principalmente en evitar las discontinuidades en los extremos del viraje, y esto puede conseguirse simplemente, por ejemplo, insertando segmentos de transición cortos sobre los cuales el ángulo de alabeo cambia linealmente con la distancia. Solo en el caso especial de que un viraje particular pueda tener un efecto dominante en las curvas de nivel de ruido finales, sería necesario modelizar las dinámicas de la transición de forma más realista, a fin de relacionar el ángulo de alabeo con tipos de aviones particulares y adoptar proporciones de balanceo apropiadas. En este contexto es suficiente poner de manifiesto que los subarcos finales Δξ_trans en cualquier viraje dependen de los requisitos de cambio del ángulo de alabeo. El resto del arco con cambio de rumbo de Δξ – 2 · Δξ_trans grados se divide en subarcos n_sub según la ecuación:

n_sub = int(1 + (Δξ – 2 · Δξ_trans)/30)

(2.7.3)

donde int(x) es una función que devuelve la parte entera de x. Entonces, el cambio de rumbo Δξ_sub de cada subarco se calcula como

Δξ_sub = (Δξ – 2 · Δξ_trans)/n_sub

(2.7.4)

donde n_sub necesita ser lo suficientemente grande como para garantizar que Δξ_sub ≤ 30 grados. La segmentación de un arco (excluidos los subsegmentos de transición de terminación) se ilustra en la figura 2.7.f¹⁶.

¹⁶ Definida de esta forma sencilla, la longitud total de la trayectoria segmentada es ligeramente inferior a la de la trayectoria circular. No obstante, el error en las curvas de nivel de ruido consecuente es insignificante si los incrementos angulares son inferiores a 30º.

Figura 2.7.f

Construcción de los segmentos de la trayectoria del vuelo que dividen el viraje en segmentos de longitud Δs (vista superior en el plano horizontal, vista inferior en el plano vertical)

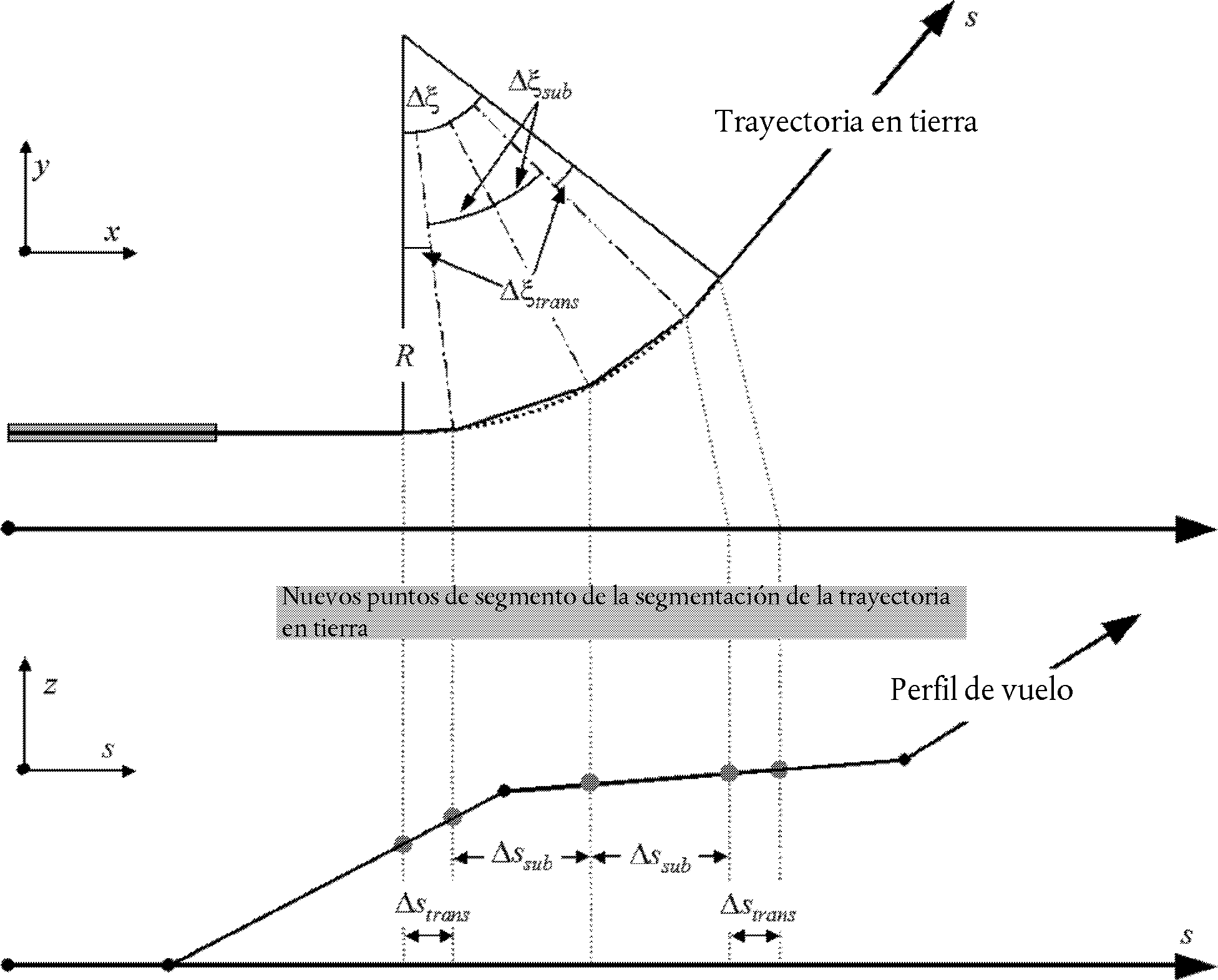
Perfil del vuelo.

Los parámetros que describen cada segmento del perfil del vuelo al inicio (sufijo 1) y al final (sufijo 2) del segmento son:

s₁, s₂ distancia a lo largo de la trayectoria en tierra,

z₁, z₂ altura del avión,

V₁, V₂ velocidad respecto a tierra,

P₁, P₂ parámetro de potencia relacionado con el ruido (de acuerdo con las curvas de NPD),

ε₁, ε₂ ángulo de alabeo.

Para crear un perfil de vuelo a partir de un conjunto de etapas del procedimiento (síntesis de la ruta del vuelo), los segmentos se crean en secuencias para conseguir las condiciones necesarias en los puntos finales. Los parámetros de los puntos finales para cada segmento se convierten en los parámetros de los puntos iniciales para cada segmento siguiente. En el cálculo de cualquier segmento, los parámetros se conocen; las condiciones necesarias del punto final se especifican en la etapa del procedimiento. Las etapas están definidas en la información por defecto ANP, o bien los define el usuario (por ejemplo, a partir de los manuales de vuelo). Las condiciones finales suelen ser la altura y la velocidad; la tarea de creación de perfiles consiste en determinar al distancia de la trayectoria cubierta para alcanzar dichas condiciones. Los parámetros no definidos se determinan mediante los cálculos de rendimiento del vuelo descritos en el apéndice B.

Si la trayectoria en tierra es recta, los puntos del perfil y los parámetros del vuelo asociados pueden determinarse con independencia de la trayectoria en tierra (el ángulo de alabeo siempre es cero). No obstante, es raro que las trayectorias en tierra sean rectas; suelen incorporar virajes y, para conseguir los mejores resultados, tienen que contabilizarse al determinar el perfil de vuelo bidimensional, cuando proceda, dividiendo los segmentos del perfil en los nodos de la trayectoria en tierra para introducir cambios del ángulo de alabeo. Por norma general, la longitud del siguiente segmento se desconoce desde el principio y se calcula suponiendo provisionalmente que no se produce ningún cambio en el ángulo de alabeo. Si se observa que el segmento provisional abarca uno o varios nodos de la trayectoria en tierra, el primero en s, es decir, s₁ < s < s₂, el segmento se trunca en s, calculando ahí los parámetros mediante interpolación (véase a continuación). Estos se convierten en los parámetros de los puntos finales del segmento actual y los parámetros de los puntos iniciales de un nuevo segmento ‒que conservan las mismas condiciones finales objetivo‒. Si no hay ningún nodo de la trayectoria en tierra que intervenga, se confirma el segmento provisional.

Si se ignoran los efectos de los virajes en el perfil de vuelo, se adopta la solución de un único segmento en vuelo recto, aunque se conserva la información del ángulo de alabeo para un uso posterior.

Independientemente de que los efectos del viraje se modelicen completamente o no, cada trayectoria de vuelo tridimensional se genera mediante la combinación de su perfil de vuelo bidimensional con su trayectoria en tierra bidimensional. El resultado es una secuencia de conjuntos de coordenadas (x,y,z), y cada una ellas es un nodo de la trayectoria en tierra segmentada, un nodo del perfil de vuelo o ambos, y los puntos del perfil van acompañados de los valores correspondientes de altura z, velocidad respecto al suelo V, ángulo de alabeo ε y potencia del motor P. Para un punto de la vía (x,y) que se encuentra entre los puntos finales de un segmento del perfil del vuelo, los parámetros del vuelo se interpolan como sigue:

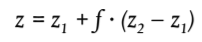
(2.7.5)

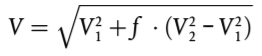
(2.7.6)

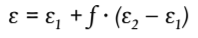
(2.7.7)

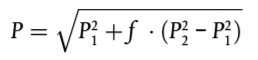
(2.7.8)

donde

f = (s – s₁)/(s₂ – s₁)

(2.7.9)

Téngase en cuenta que, mientras que se supone que z y ε varían linealmente con la distancia, se supone que V y P varían linealmente con el tiempo (es decir, con una aceleración constante¹⁷).

¹⁷ Incluso aunque el reglaje de la potencia del motor se mantenga constante a lo largo de un segmento, la fuerza propulsora y la aceleración pueden cambiar debido a la variación de la densidad del aire con la altura. No obstante, a efectos de la modelización del ruido, estos cambios suelen ser insignificantes.

Al asociar los segmentos del perfil del vuelo con los datos de radar (análisis de la trayectoria del vuelo), todas las distancias de los puntos finales, las alturas, las velocidades y los ángulos de alabeo se determinan directamente a partir de dichos datos; solo el régimen de potencia tiene que calcularse conforme a las ecuaciones de rendimiento. Habida cuenta de que las coordenadas del perfil de vuelo y de la trayectoria en tierra se pueden asociar según corresponda, suele tratarse de una tarea bastante sencilla.

Segmentación del desplazamiento en tierra firme al despegar.

Al despegar, a medida que el avión acelera entre el punto en que se libera el freno (lo que también se conoce como punto de partida de rodaje, SOR) y el punto de despegue, la velocidad cambia radicalmente en una distancia comprendida entre 1.500 y 2.500 m, desde cero hasta un rango comprendido entre 80 y 100 m/s.

El empuje al despegar se divide en segmentos con longitudes variables y, con respecto a cada una de ellas, la velocidad del avión cambia en incrementos específicos ΔV de no más de 10 m/s (en torno a 20 kt). Aunque realmente varía durante el rodaje al despegar, se considera que una hipótesis de aceleración constante es adecuada para este propósito. En este caso, para la fase de despegue, V₁ es la velocidad inicial, V₂ es la velocidad de despegue, n_TO es el número de segmentos de despegue y s_TO es la distancia de despegue equivalente s_TO. Para la distancia de despegue equivalente s_TO (véase el apéndice B), la velocidad inicial V₁ y la velocidad de despegue V_T2, el número n_TO de segmentos para el desplazamiento en tierra firme es:

n_TO = int(1 + (V₂ – V₁)/10)

(2.7.10)

y, en consecuencia, el cambio de velocidad a lo largo del segmento es:

ΔV = (V₂ – V₁)/n_TO

(2.7.11)

y el tiempo Δt en cada segmento (suponiendo una aceleración constante) es:

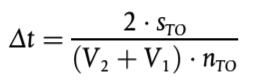
(2.7.12)

La longitud s_TO,k del segmento k (1 ≤ k ≤ n_TO) del rodaje al despegar es:

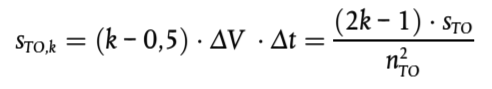
(2.7.13)

Ejemplo:

Para una distancia de despegue s_TO = 1 600 m, V₁ = 0 m/s y V₂ = 75 m/s, esto resulta en n_TO = 8 segmentos con longitudes que oscilan entre 25 y 375 metros (véase la figura 2.7.g):

Figura 2.7.g

Segmentación del rodaje de despegue (ejemplo para ocho segmentos)

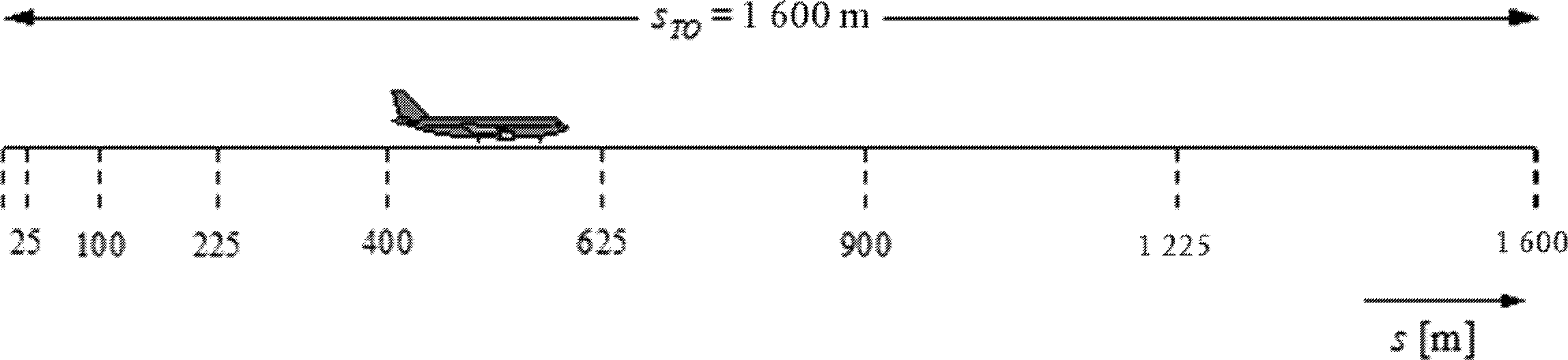
Al igual que sucede con los cambios de velocidad, el empuje del avión cambia a lo largo de cada segmento mediante un incremento constante ΔP, que se calcula como:

ΔP = (P_TO – P_init)/n_TO

(2.7.14)

donde P_TO y P_init, respectivamente, designan el empuje del avión en el punto de despegue y el empuje del avión al punto de partida de rodaje de despegue.

El uso de este incremento de empuje constante (en lugar del uso de la ecuación de forma cuadrática 2.7.8) pretende ser coherente con la relación lineal entre el empuje y la velocidad en el caso de un avión con motor a reacción (ecuación B-1).

Segmentación del segmento de ascenso inicial.

Durante el segmento de ascenso inicial, la geometría cambia rápidamente, en particular con respecto a las ubicaciones del observador en el lado de la trayectoria del vuelo, donde el ángulo beta cambiará rápidamente a medida que el avión asciende a lo largo del segmento inicial. Las comparaciones con cálculos de segmentos muy pequeños revelan que un único segmento de ascenso ofrece una aproximación muy pobre al cálculo del ruido en puntos situados en los laterales de la trayectoria del vuelo. La precisión del cálculo se mejora mediante la subsegmentación del primer segmento de despegue. La atenuación lateral influye significativamente en la longitud de cada segmento y en el número. Teniendo en cuenta la expresión de la atención lateral total del avión con motores montados en fuselaje, se puede observar que, para un cambio limitado de la atenuación lateral de 1,5 dB por subsegmento, el segmento de ascenso inicial debe subsegmentarse en función del siguiente conjunto de valores de altura:

z = {18,9; 41,5; 68,3; 102,1; 147,5; 214,9; 334,9; 609,6; 1 289,6} metros, o

z = {62, 136, 224, 335, 484, 705, 1 099, 2 000, 4 231} pies

Las alturas anteriores se aplican identificando qué altura de entre las anteriores está más próxima al punto final del segmento original. Las alturas reales del subsegmento se calcularían de la siguiente forma:

z′_i = z [z_i/z_N] (i = 1…N)

(2.7.15)

donde z es la altura del extremo del segmento original, z_i es la altura i del conjunto de valores de alturas y z_N es el límite superior más próximo a la altura z. Este proceso a lugar a que el cambio de atenuación lateral a lo largo de cada segmento sea constante, obteniéndose las curvas de nivel de ruido más precisas, pero sin el coste que supone utilizar segmentos muy cortos.

Ejemplo:

Si la altura del punto final del segmento original está en z = 304,8 m, entonces de acuerdo con el conjunto de valores de altura, 214,9 < 304,8 < 334,9 y el límite superior más próximo a z = 304,8 m, es z₇ = 334,9 m. Por tanto, las alturas de los puntos finales del subsegmento se calculan como sigue:

z_i′ = 304,8 [z_i/334,9] (i = 1…N)

Por tanto, z_i′ sería 17,2 m y z_2i′ sería 37,8 m, etc.

Los valores de velocidad y potencia del motor en los puntos insertados se interpolan usando las ecuaciones (2.7.11) y (2.7.13), respectivamente.

Segmentación de los segmentos en vuelo.

Después de obtener la trayectoria del vuelo segmentado conforme al procedimiento descrito en la sección 2.7.13 y de aplicar la subsegmentación descrita, puede resultar necesario realizar ajustes adicionales de segmentación. Estos ajustes incluyen:

‒ la eliminación de los puntos de la trayectoria del vuelo que están muy próximos entre sí;

‒ la inserción de puntos adicionales si la velocidad cambia a lo largo de los segmentos que son demasiado largos.

Cuando dos puntos adyacentes se encuentran a menos de 10 metros, y si las velocidades y los empujes asociados son los mismos, es necesario eliminar uno de los puntos.

Para los segmentos en vuelo en los que hay un cambio de velocidad importante a lo largo de un segmento, debe subdividirse como en el desplazamiento en tierra firme, es decir

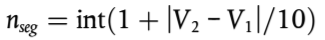
(2.7.16)

donde V₁ y V₂ son las velocidades iniciales y finales del segmento, respectivamente. Los parámetros del subsegmento correspondiente se calculan de manera similar al desplazamiento en tierra firme al despegar, usando las ecuaciones de 2.7.11 a 2.7.13.

Rodaje en tierra en los aterrizajes.

Aunque el rodaje en tierra para el aterrizaje es básicamente una inversión del rodaje en tierra para el despegue, es necesario tener especialmente en cuenta:

‒ el empuje inverso, que a veces se aplica para desacelerar el avión;

‒ los aviones que dejan la pista después de la desaceleración (el avión que deja la pista deja de contribuir al ruido del aire, ya que se ignora el ruido de «taxiing»).

En comparación con la distancia de rodaje de despegue, que se obtiene a partir de los parámetros del rendimiento del avión, la distancia de parada s_stop (es decir, la distancia desde el aterrizaje hasta el punto en que el avión sale de la pista) no es puramente específica del avión. Aunque se puede calcular una distancia de parada mínima a partir del rendimiento y la masa del avión (y el empuje inverso disponible), la distancia de parada real depende también de la ubicación de las pistas de rodaje, de la situación del tráfico y de los reglamentos específicos del aeropuerto que rigen el uso del empuje inverso.

El uso del empuje inverso no es un procedimiento estándar; solo se aplica si no se puede conseguir la desaceleración necesaria mediante la utilización de los frenos de las ruedas. (El empuje inverso puede resultar realmente molesto, ya que un cambio rápido de la potencia del motor del ralentí al ajuste inverso produce un estruendo de ruido).

No obstante, la mayoría de las pistas se usan para los despegues y los aterrizajes, ya que el empuje inverso tiene un efecto mínimo en los contornos de ruido, habida cuenta de que la energía sonora total en las proximidades de la pista está dominada por el ruido producido por las operaciones de despegue. Las contribuciones del empuje inverso a las curvas de nivel de ruido solo pueden resultar significativas cuando el uso de la pista está limitado a las operaciones de aterrizaje.

Físicamente, el ruido del empuje inverso es un proceso muy complejo, pero, debido al hecho de que tiene una importancia relativamente baja para el cálculo de las isófonas, se puede modelizar de manera sencilla ‒el cambio rápido de la potencia del motor se tienen en cuenta mediante una segmentación adecuada‒.

Es evidente que la modelización del empuje en tierra al aterrizar es menos complicada que para el ruido del empuje al despegar. Se recomiendan los siguientes supuestos de modelización simplificada para uso general, siempre que no haya información detallada disponible (véase la figura 2.7.h).

Figura 2.7.h

Modelización del empuje en tierra al aterrizar

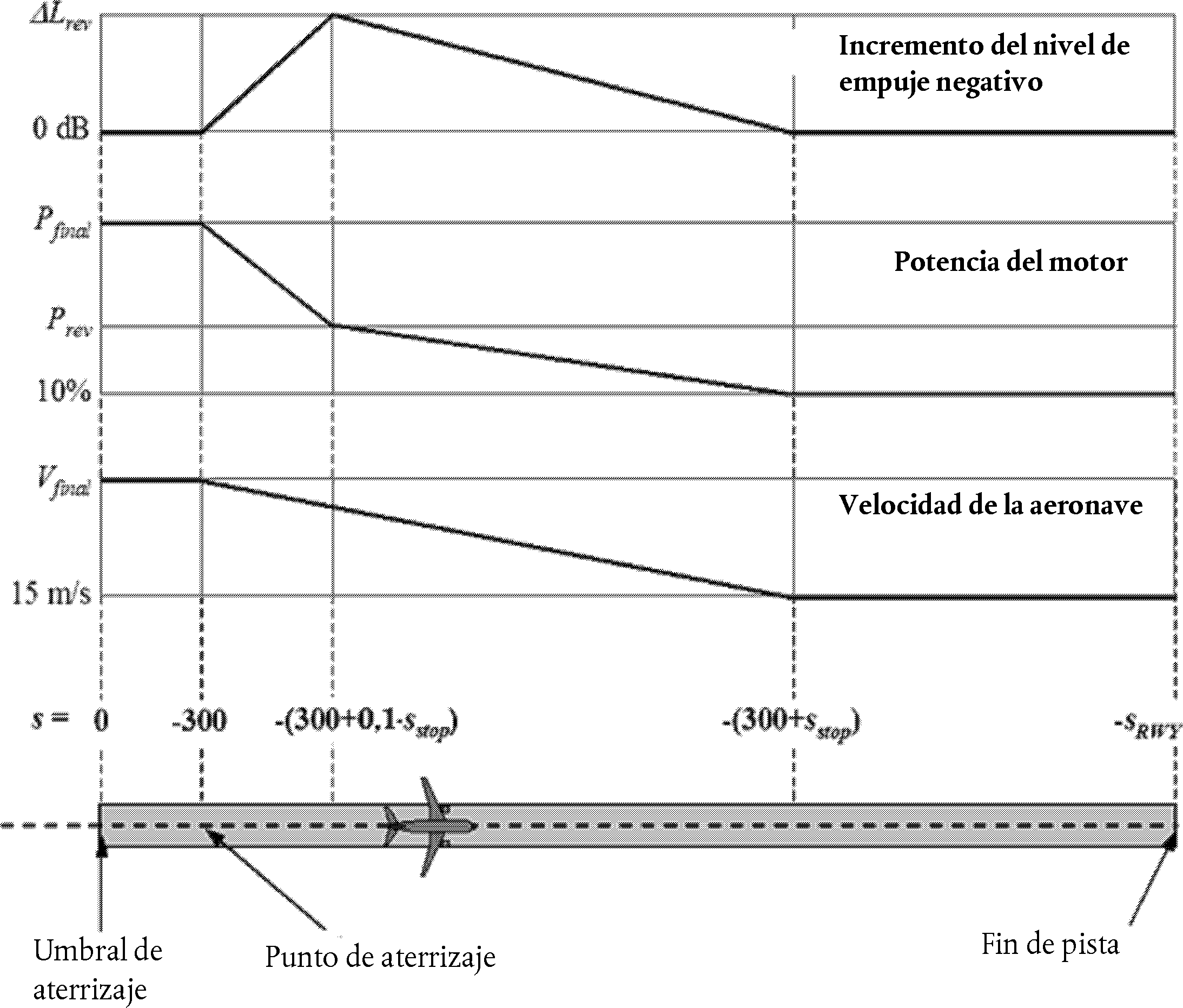
El avión aterriza 300 metros más allá del umbral de aterrizaje (que tiene la coordenada s = 0 a lo largo de la trayectoria en tierra de aproximación). A continuación, el avión se desacelera a lo largo de la distancia de parada s_stop ‒los valores específicos del avión se facilitan en la base de datos ANP‒ a partir de la velocidad de aproximación final V_final hasta 15 m/s. Habida cuenta de los rápidos cambios de velocidad a lo largo de este segmento, debe subsegmentarse de la misma forma que para el desplazamiento en tierra firme al despegar (segmentos en vuelo con cambios rápidos de velocidad), usando las ecuaciones de 2.7.10 a 2.7.13.

La potencia del motor cambia de una potencia de aproximación final al aterrizar a un reglaje de la potencia de empuje inverso P_rev a lo largo de una distancia de 0,1×s_stop, a continuación, disminuye al 10 % de la potencia máxima disponible a lo largo del 90 % restante de la distancia de parada. Hasta el final de la pista (a s = –s_RWY), la velocidad del avión permanece constante.

Las curvas NPD para el empuje inverso actualmente no están incluidas en la base de datos de ANP y, por tanto, es necesario utilizar en las curvas convencionales para modelizar este efecto. Normalmente, la potencia de empuje inverso P_rev ronda el 20 % del reglaje de la potencia total, y esto se recomienda usar este valor cuando no hay disponible información operativa. No obstante, con un reglaje de la potencia determinado, el empuje inverso tiende a generar mucho más ruido que el empuje de propulsión, y es necesario aplicar un incremento ΔL al nivel del evento de las tablas NPD, de manera que aumente desde cero hasta un valor ΔL_rev (se recomienda provisionalmente un valor de 5 dB¹⁸) a lo largo de 0,1×s_stop y, a continuación, disminuye linealmente hasta cero durante el resto de la distancia de parada.

¹⁸ Esto se recomendó en la edición anterior de CEAC, Doc 29, pero aún se considera provisional pendiente de la adquisición de más datos experimentales corroborativos.

2.7.14. Cálculo de ruido de un único evento.

El núcleo del proceso de modelización, descrito aquí íntegramente, es el cálculo del nivel del evento de ruido a partir de la información de la trayectoria del vuelo descrita en las secciones 2.7.7 a 2.7.13.

2.7.15. Índices de un único evento.

El sonido generado por el movimiento de un avión en la ubicación del observador se expresa como un «nivel sonoro (ruido) de un evento único», que es un indicador de su impacto sobre las personas. El sonido recibido se mide en términos de ruido mediante una escala de decibelios básica L_(t) que aplica una ponderación de frecuencias (o filtro) para simular las características del oído humano. La escala más importante usada en la modelización de las curvas de nivel de ruido de las aeronaves es el nivel acústico ponderado A, L_A.

La métrica que se usa con mayor frecuencia para describir eventos completos es «el nivel sonoro de exposición sonora de un evento único», L_E, que tienen en cuenta toda la energía sonora de los eventos (o la mayor parte de esta energía). Para la elaboración de disposiciones para la integración temporal necesaria para su obtención, implica un aumento de las complejidades principales de la modelización de la segmentación (o simulación). Más sencillo de modelizar es otro índice alternativo L_max que es el nivel máximo instantáneo que se produce durante el evento; no obstante, L_E es el componente básico de los índices modernos de ruido de aeronaves, y en el futuro se pueden esperar modelos prácticos que engloben ambos índices L_max y L_E. Cualquier índice puede medirse con diferentes escalas de ruido; en este documento, solo se considera el nivel sonoro con ponderación A. Simbólicamente, la escala se indica generalmente mediante el subíndice A, es decir, L_AE, L_Amax.

El nivel de exposición sonora (de ruido) de un único evento se expresa exactamente como:

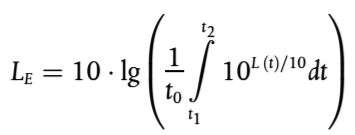
(2.7.17)

donde t₀ denota un tiempo de referencia. Se elige el intervalo de integración [t₁,t₂] para garantizar que se abarca (casi) todo el sonido pertinente del evento. Muy a menudo, se eligen los límites t₁ y t₂ para abarcar el período para el que el nivel de L_(t) se encuentra dentro de L_max ‒ 10 dB. Este período se conoce como el tiempo «10 dB por debajo el máximo». Los niveles de exposición sonora tabulados en la base de datos ANP son valores 10 dB por debajo el máximo¹⁹.

¹⁹ L_E 10 dB por debajo del máximo puede ser 0,5 dB más bajo que el valor de L_E evaluado durante más tiempo. No obstante, salvo en distancias oblicuas cortas donde los niveles del evento son altos, ruidos ambientales extraños a menudo hacen que los intervalos de medida más largos resulten poco prácticos, y los valores 10 dB por debajo del máximo son la norma. Como los estudios de los efectos del ruido (usados para «calibrar» los contornos de ruido) también tienden a basarse en valores 10 dB por debajo del máximo, las tabulaciones ANP se consideran totalmente convenientes.

Para la modelización de las curvas de nivel de ruido de una aeronave, la aplicación principal de la ecuación 2.7.17 utilizada es el índice normalizado nivel de exposición al ruido L_AE (acrónimo SEL):

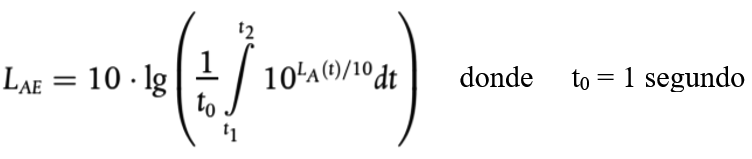
(2.7.18)

Las ecuaciones del nivel de exposición anteriores pueden usarse para determinar los niveles del evento cuando se conoce toda la historia temporal L_(t). Dichos historiales de tiempo no se definen en la metodología de modelización de ruido recomendada; los niveles de exposición de los eventos se calculan sumando los valores de los segmentos; los niveles de ruido de los eventos parciales, correspondientes a cada uno de ellos definen la contribución de un único segmento finito de la trayectoria del vuelo.

2.7.16. Determinación de los niveles del evento a partir de los datos NPD.

La fuente principal de datos sobre el ruido de los aviones es la base de datos internacional de rendimiento y ruido de las aeronaves (ANP). En ella figuran los valores de L_max y L_E en función de la distancia de propagación d para tipos de aviones específicos, variantes, configuraciones del vuelo (aproximación, salida, flaps) y reglaje de la potencia P. Están relacionados con un vuelo uniforme a velocidades de referencia específicas V_ref a lo largo de una trayectoria de vuelo recta supuestamente infinita²⁰.

²⁰ Aunque la noción de una trayectoria de vuelo de longitud infinita es importante para definir el nivel de exposición al ruido del evento L_E, guarda menor relevancia en el caso del nivel máximo del evento L_max que se rige conforme al ruido emitido por el avión en una posición particular en el punto más próximo (o cerca) al observador. A efectos de modelización, el parámetro de distancia NPD se considera como la distancia mínima entre el observador y el segmento.

Más adelante se describe la forma en que se especifican las variables independientes P y d. En una única búsqueda, con los valores de entrada P y d, los valores de salida necesarios son los niveles básicos L_max(P,d) o L_E∞(P,d) (aplicables a una trayectoria de vuelo infinita). A menos que los valores resulten estar tabulados exactamente para P o d, por norma general resultará necesario calcular los niveles necesarios de ruido del evento mediante la interpolación. Se usa una interpolación lineal entre el reglaje de la potencia tabulada, mientras que se utiliza una interpolación logarítmica entre las distancias tabuladas (véase la figura 2.7.i).

Figura 2.7.i

Interpolación en las curvas ruido-potencia-distancia

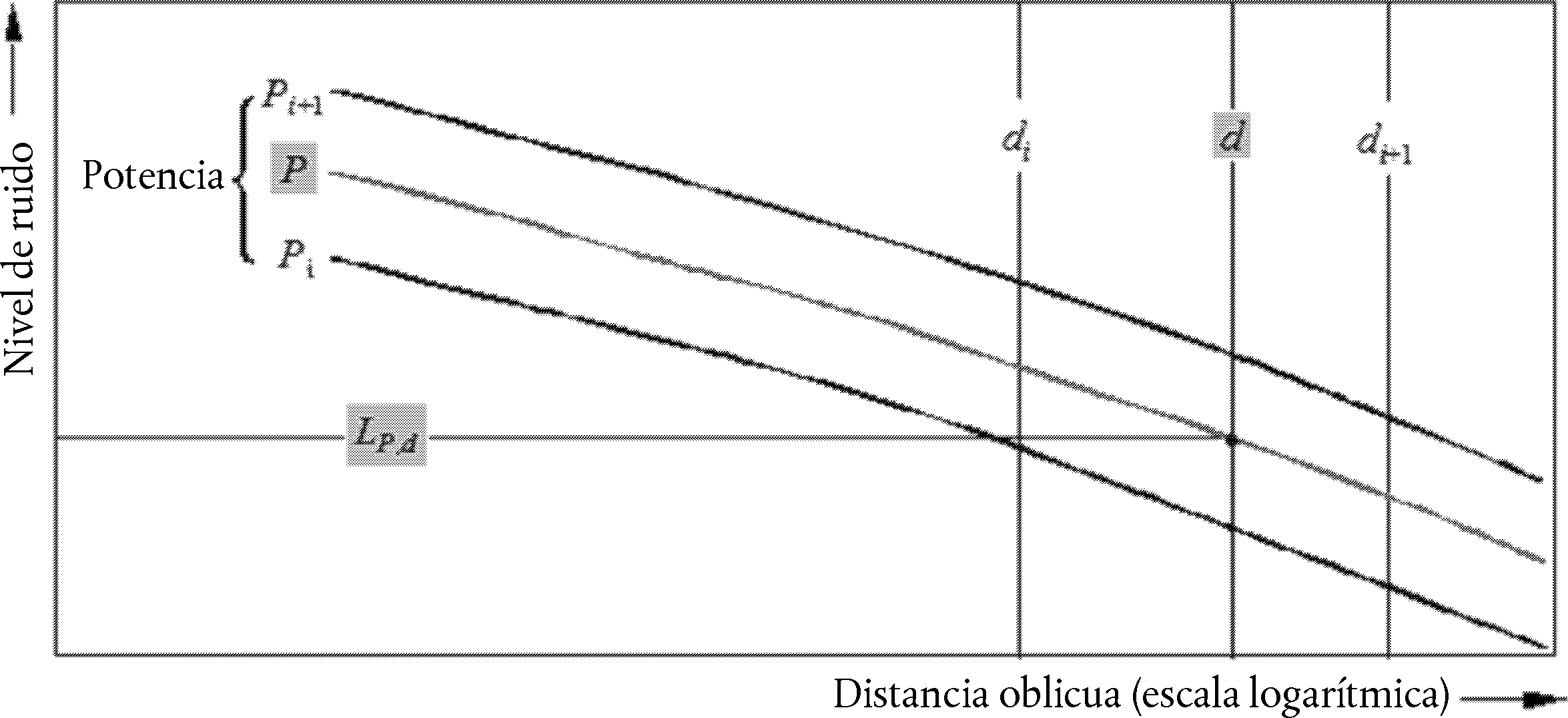
Si P_i y P_{i + 1} son valores de potencia del motor para los que se tabula el nivel de ruido con respecto a los datos de distancia, el nivel de ruido L(P) a una distancia determinada para la potencia intermedia P, entre P_i y P_{i + 1}, resulta de:

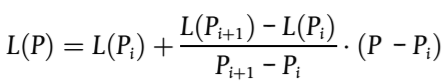
(2.7.19)

Si, con cualquier reglaje de la potencia, d_i y d_{i + 1} son distancias para las cuales se tabulan los datos de ruido, el nivel de ruido L(d) para una distancia intermedia d, entre d_i y d_{i + 1} resulta de:

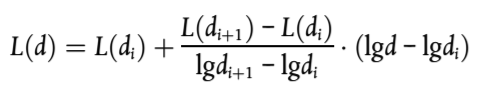
(2.7.20)

Con las ecuaciones (2.7.19) y (2.7.20), se puede obtener un nivel de ruido L(P,d) para cualquier reglaje de la potencia P y a cualquier distancia d contemplada en la base de datos NPD.

Para distancias d que queden fuera del marco de NPD, se usa la ecuación 2.7.20 para realizar la extrapolación de los últimos dos valores, es decir, llegadas desde L(d₁) y L(d₂) o salidas desde L(d_{I – 1}) y L(d_I), donde I es el número total de puntos NPD en la curva.

Por tanto,

Llegadas: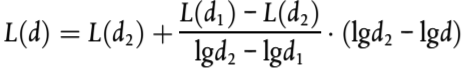

(2.7.21)

Salidas: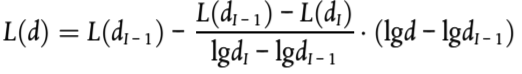

(2.7.22)

Habida cuenta de que, a cortas distancias d, los niveles de ruido aumentan con mucha rapidez a medida que disminuye la distancia de propagación, se recomienda imponer un límite inferior de 30 m para d, es decir, d = max (d, 30 m).

Ajuste de impedancia de datos NPD estándar.

Los datos NPD facilitados en la base de datos de ANP se normalizan para condiciones atmosféricas específicas (temperatura de 25 °C y presión de 101,325 kPa). Antes de aplicar el método de interpolación/extrapolación descrito anteriormente, debe aplicarse un ajuste de impedancia acústica a estos datos NPD estándar.

La impedancia acústica está relacionada con la propagación de las ondas sonoras en un medio, y se define como el producto de la densidad del aire y la velocidad del sonido. Para una intensidad sonora determinada (energía por unidad de superficie) percibida a una distancia específica de la fuente, la presión sonora asociada (usada para definir los índices SEL y L_Amax) depende de la impedancia acústica del aire en la ubicación de medida. Es una función de la temperatura y la presión atmosférica (y de la altitud indirectamente). Por tanto, es necesario ajustar los datos NPD estándar de la base de datos ANP para tener en cuenta las condiciones reales de temperatura y presión en el punto del receptor, que difieren significativamente de las condiciones normalizadas de los datos ANP.

El ajuste de impedancia que ha de aplicarse a los niveles estándar NPD se expresa como sigue:

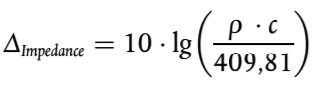
(2.7.23)

donde:

Δ_Impedance: Ajuste de impedancia para las condiciones atmosféricas reales en el punto del receptor (dB)

ρ · c: Impedancia acústica (newton-segundos/m³) del aire en el punto del receptor (409,81 es la impedancia asociada con las condiciones atmosféricas de referencia de los datos NPD en la base de datos ANP).

La impedancia ρ · c se calcula como sigue:

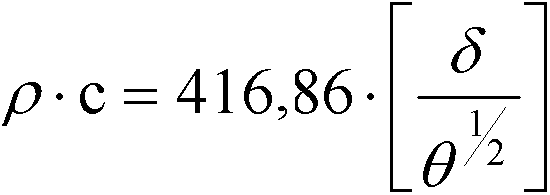
(2.7.24)

Δ: p/po, el cociente entre la presión del aire ambiente a la altitud del observador y la presión del aire estándar al nivel medio de la mar: po= 101,325 kPa (o 1 013,25 mb)

θ: (T + 273,15) / (T₀ + 273,15), el cociente entre la temperatura del aire a la altitud del observador y la temperatura del aire estándar al nivel medio de la mar: T₀ = 15,0 °C

El ajuste de impedancia acústica suele ser inferior a algunas décimas de dB. En particular, cabe destacar que, en condiciones atmosféricas estándar (po = 101,325 kPa y T₀ = 15,0 °C), el ajuste de impedancia es inferior a 0,1 dB (0,074 dB). No obstante, cuando hay una variación importante de temperatura y de presión atmosférica en relación con las condiciones atmosféricas de referencia de los datos NPD, el ajuste puede resultar más importante.

2.7.17. Expresiones generales.

Nivel del evento del segmento, L_seg.

Los valores para un segmento se determinan mediante la aplicación de ajustes a los valores básicos (trayectoria infinita) que se obtienen en los datos NPD. El nivel de ruido máximo de un segmento de la trayectoria de un vuelo L_max,seg se puede expresar en general como:

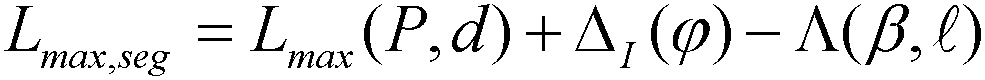
(2.7.25)

y la contribución de un segmento de la trayectoria de un vuelo a L_E, como:

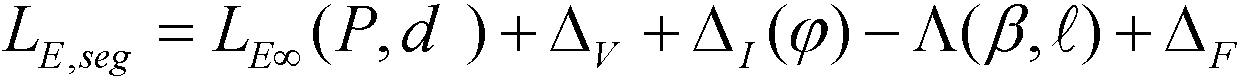
(2.7.26)

Los «términos de corrección» de las ecuaciones 2.7.25 y 2.7.26 ‒que se describen detalladamente en la sección 2.7.19‒ tienen en cuenta los siguientes efectos:

Δ_V: Corrección de la duración: los datos NPD corresponden a una velocidad del vuelo de referencia. Esta corrección ajusta los niveles de exposición a velocidades que no son la de referencia. (No se aplica a L_max,seg).

Δ_I(φ): Efecto de la instalación: describe una variación de la directividad lateral debido al blindaje, la refracción y la reflexión causados por el fuselaje, y los campos de flujo de los motores y su entorno.

Λ(β,ℓ): Atenuación lateral: se trata de un elemento importante en la propagación del sonido a ángulos bajos respecto a la superficie del terreno; tiene en cuenta la interacción entre las ondas sonoras directas y reflejadas (efecto de suelo) y para los efectos de la falta de uniformidad atmosférica (causada principalmente por el terreno) que refractan las ondas sonoras a medida que viajan hacia el observador por los lados de la trayectoria del vuelo.

Δ_F: Corrección de segmentos finitos (fracción de ruido): tiene en cuenta la longitud finita del segmento que obviamente contribuye menos a la exposición al ruido que una infinita. Solo se aplica a los índices de exposición.

Si el segmento forma parte del desplazamiento en tierra firme en el despegue o el aterrizaje y el observador se encuentra detrás del segmento objeto de estudio, se aplican cálculos especiales para representar la direccionalidad pronunciada del ruido del motor a reacción que se observa debajo de un avión a punto de despegar. Estos cálculos especiales se concretan, en particular en el uso de una expresión particular del cálculo del ruido para la exposición al ruido:

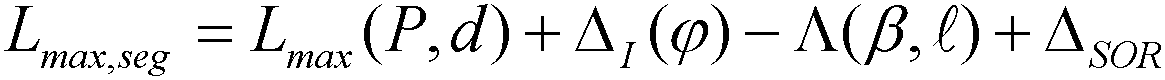
(2.7.27)

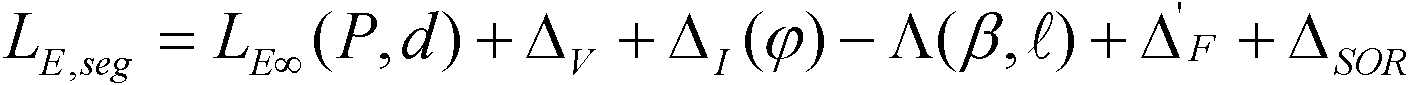
(2.7.28)

Δ′_F: Expresión particular de la corrección del segmento.

Δ_SOR: Corrección de la directividad: representa la direccionalidad pronunciada del ruido del motor a reacción detrás del segmento del desplazamiento en tierra firme.

El tratamiento específico de los segmentos de desplazamiento en tierra firme se describe en la sección 2.7.19. En las secciones siguientes se describe el cálculo de los niveles de ruido del segmento.

Nivel de ruido de un evento L del movimiento de un avión.

El nivel máximo L_max sencillamente es el valor máximo de los valores del segmento L_max,seg (véanse las ecuaciones 2.7.25 y 2.7.27)

L_max = max(L_max,seg)

(2.7.29)

donde el valor de cada segmento se determina a partir de los datos NPD para la potencia P y la distancia d. Estos parámetros y los términos modificadores Δ_I (φ) y Λ(β,ℓ) se explican a continuación.

El nivel de exposición L_E se calcula como la suma de decibelios de las contribuciones L_E,seg de cada segmento significativo desde el punto de vista del ruido de su trayectoria de vuelo; es decir,

(2.7.30)

La suma se realiza paso a paso para cada uno de los segmentos de la trayectoria del vuelo.

El resto de este capítulo se dedica a la determinación de los niveles de ruido de los segmentos L_max,seg y L_E,seg.

2.7.18. Parámetros de los segmentos de las trayectorias de vuelo.

La potencia P, y la distancia d, para las que se interpolan los niveles básicos L_max,seg(P,d) y L_E∞(P,d) a partir de tablas NPD, se determinan a partir de los parámetros geométricos y operativos que definen el segmento. La forma de hacerlo se explica a continuación con la ayuda de ilustraciones referidas al plano, que contiene el segmento y el observador.

Parámetros geométricos.

En las figuras 2.7.j a 2.7.l se muestran las geometrías fuente-receptor cuando el observador O está a) detrás, b) junto a y (c) delante del segmento S₁S₂, donde la dirección del vuelo va de S₁ a S₂. En estos diagramas

O: es la ubicación del observador.

S₁ y S₂: representan el inicio y el final del segmento.

S_p: es el punto situado en el segmento o en su extensión, donde se produce el corte con la perpendicular trazada desde el observador.

d₁ y d₂: son las distancias entre el inicio del segmento y el fin del segmento y el observador.

d_s: es la distancia más corta entre el observador y el segmento.

d_p: es la distancia perpendicular entre el observador y el segmento ampliado (distancia oblicua mínima).

λ: es la longitud del segmento de la trayectoria del vuelo.

q: es la distancia desde S₁ a S_p (negativa si la posición del observador está detrás del segmento).

Figura 2.7.j

Geometría del segmento de la trayectoria del vuelo para el observador por detrás del segmento

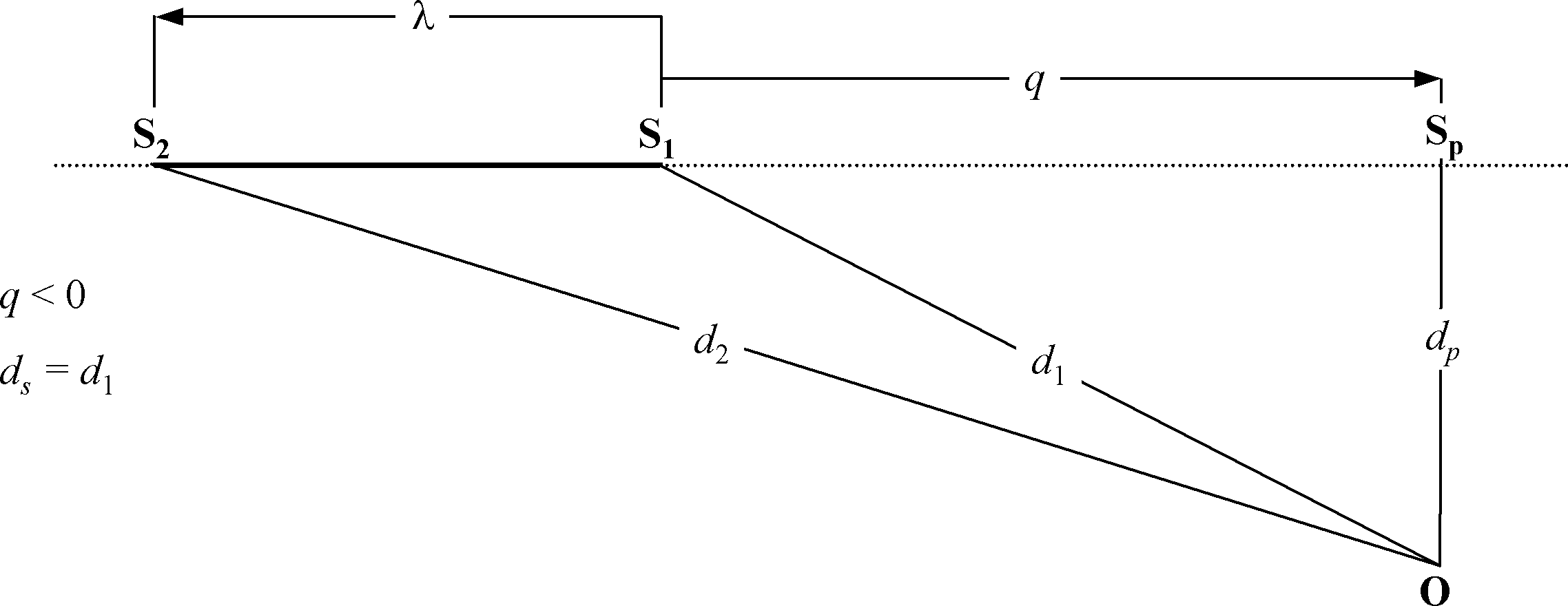
Figura 2.7.k

Geometría del segmento de la trayectoria del vuelo para el observador a lo largo del segmento

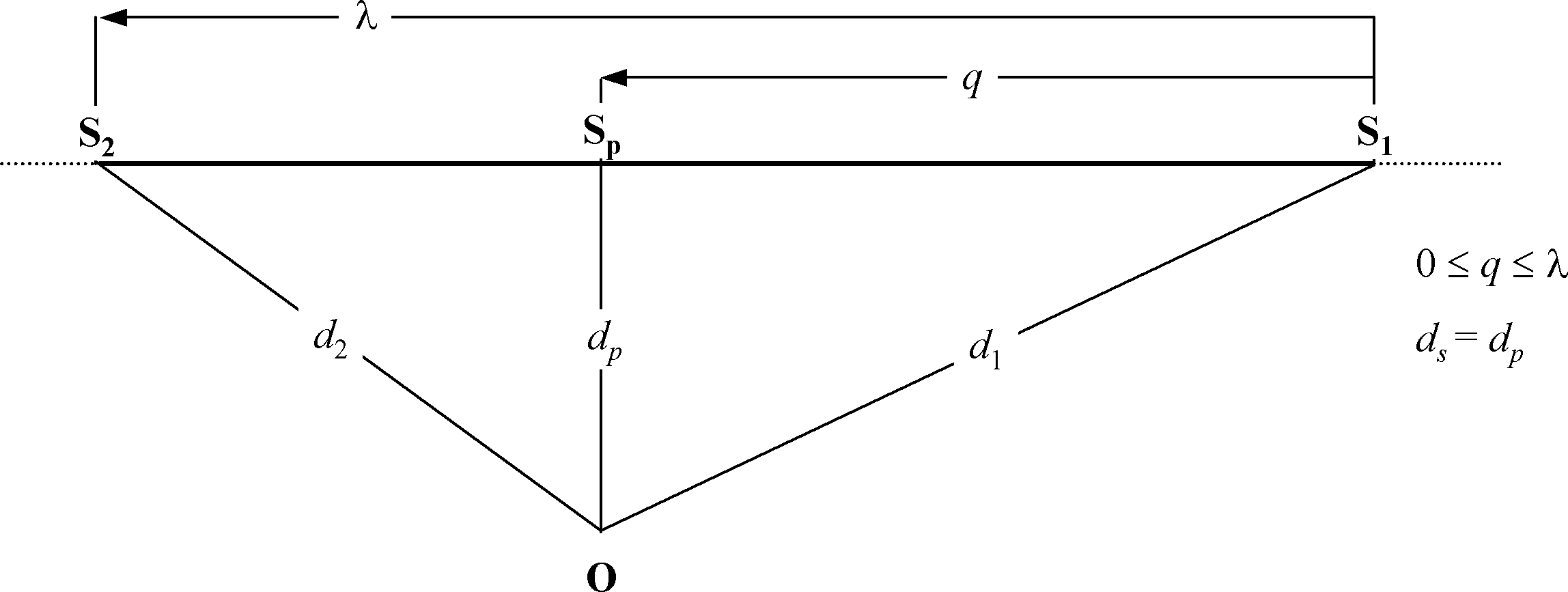
Figura 2.7.l

Geometría del segmento de la trayectoria del vuelo para el observador delante del segmento

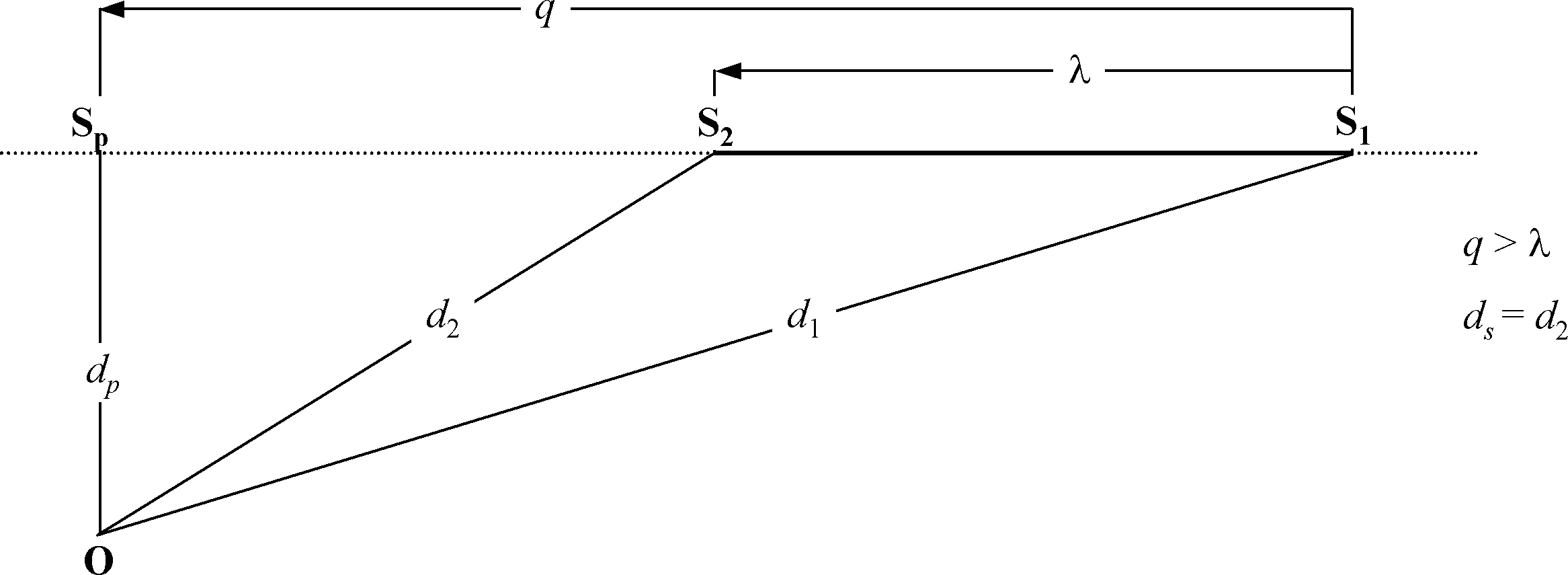
El segmento de la trayectoria del vuelo se representa mediante una línea continua en negrita. La línea discontinua representa la extensión de la trayectoria del vuelo que se extiende hasta el infinito en ambas direcciones. Para los segmentos en vuelo, cuando el índice del evento es un nivel de exposición L_E, el parámetro de la distancia NPD d es la distancia d_p entre S_p y el observador, denominada distancia oblicua mínima (es decir, la distancia perpendicular desde el observador hasta el segmento o su extensión, en otras palabras hasta la trayectoria de vuelo infinita ‒hipotética‒ de la que se considera que el segmento forma parte.

No obstante, en el caso de índices del nivel de exposición donde las ubicaciones del observador están detrás de los segmentos terreno durante el rodaje del despegue y las ubicaciones delante de los segmentos terreno durante el rodaje del aterrizaje, el parámetro de la distancia NPD d se convierte en la distancia d_s, la distancia más corta desde el observador al segmento (es decir, lo mismo que para los índices de nivel máximo).

Para los índices de nivel máximo, el parámetro de la distancia NPD d es d_s, la distancia más corta desde el observador hasta el segmento.

Potencia del segmento P.

Los datos NPD tabulados describen el ruido de un avión en un vuelo recto uniforme sobre una trayectoria de vuelo infinita, es decir, con una potencia constante del motor P. La metodología recomendada divide las trayectorias de vuelo, a lo largo de las cuales la velocidad y la dirección varían, en una serie de segmentos finitos, cada uno de ellos considerados partes de una trayectoria de vuelo infinita uniforme para la que los datos NPD son válidos. No obstante, la metodología prevé cambios de potencia a lo largo de la longitud del segmento; se considera que cambia linealmente con la distancia desde P₁ al inicio hasta P₂ al final. Por tanto, resulta necesario definir un valor de segmento uniforme equivalente P. Se considera como el valor en el punto del segmento más próximo al observador. Si el observador está a un lado del segmento (figura 2.7.k), se obtiene mediante la interpolación, como resultado de la ecuación 2.7.8, entre los valores finales, es decir

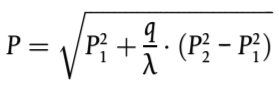
(2.7.31)

Si el observador está detrás o delante del segmento, se encuentra en el punto final más próximo, P₁ o P₂.

2.7.19. Términos de corrección del nivel del evento del segmento.

Los datos NPD definen los niveles de ruido del evento como una función de la distancia en perpendicular a una trayectoria de nivel recto idealizada de longitud infinita, por la cual un avión vuela con una potencia constante y a una velocidad de referencia fija²¹. Por tanto, el nivel del evento obtenido por interpolación de los valores tabulados en el cuadro NPD para un reglaje de la potencia específico y la distancia oblicua mínima se considera como un nivel básico. Se aplica a una trayectoria de vuelo infinita y tiene que corregirse para tener en cuenta los efectos de 1) una velocidad que no es de referencia, 2) los efectos de instalación del motor (directividad lateral), 3) la atenuación lateral, 4) la longitud de segmento finita y 5) la directividad longitudinal detrás del punto de inicio del rodaje en el despegue (véanse las ecuaciones 2.7.25 y 2.7.26).

²¹ Las especificaciones de NPD requieren que los datos se basen en las medidas del vuelo recto uniforme, no necesariamente a nivel; para crear las condiciones de vuelo necesarias, la trayectoria del vuelo del avión de prueba se puede inclinar hasta la horizontal. No obstante, como bien se observará, las trayectorias inclinadas plantean dificultades de cálculo y, al utilizar los datos para la modelización, es conveniente visualizar las trayectorias fuente como rectas y a nivel .

Corrección de la duración ΔV (solo para los niveles de exposición L_E).

Esta corrección²² tiene en cuenta un cambio de los niveles de exposición si la velocidad real respecto a tierra del segmento difiere de la velocidad de referencia del avión V_ref a la que se refieren los datos NPD. Al igual que la potencia del motor, la velocidad varía a lo largo del segmento (la velocidad respecto a tierra varía de V₁ a V₂) y es necesario definir una velocidad de segmento equivalente V_seg, recordando que el segmento está inclinado hacia el suelo; es decir:

²² Esto se conoce como la corrección de la duración, porque prevé los efectos de la velocidad del avión en la duración del evento acústico ‒con la sencilla suposición de que, si otros aspectos son iguales, la duración y, por tanto, la energía sonora del evento recibida, es inversamente proporcional a la velocidad de la fuente‒.

V_seg = V/cos

(2.7.32)

donde V es una velocidad del segmento equivalente con respecto a tierra (para obtener información, véase la ecuación B-22, que expresa V en términos de velocidad calibrada en el aire, V_c y

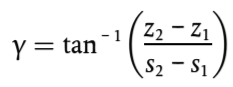
(2.7.33)

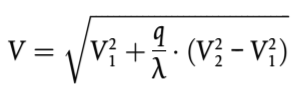
(2.7.34)

Para los segmentos aéreos, V se considera la velocidad con respecto a tierra en el punto de aproximación más cercano S, interpolada entre los valores de punto final del segmento, suponiendo que varía linealmente con el tiempo; es decir, si el observador está a un lado del segmento:

Si el observador está detrás o delante del segmento, se encuentra en el punto final más próximo, V₁ o V₂.

Para segmentos de la pista (tramos del desplazamiento en tierra firme para despegue o aterrizaje para los que γ = 0) V_seg se considera sencillamente como la media de las velocidades iniciales y finales del segmento; es decir:

V_seg = (V₁ + V₂)/2

(2.7.35)

En cualquier caso, la corrección de la duración adicional es:

Δ_V = 10 · lg(V_ref/V_seg)

(2.7.36)

Geometría de la propagación sonora.

En la figura 2.7.l se ilustra la geometría básica en el plano normal de la trayectoria del vuelo del avión. La línea de tierra es la intersección del plano normal y del plano de tierra nivelado. (Si la trayectoria del vuelo es a nivel, la línea a tierra es una vista final del plano de masa). El avión experimenta movimientos de alabeo en el ángulo ε medido en sentido contrario a las agujas del reloj sobre su eje longitudinal (es decir, ascenso del semiala de estibor). Por tanto, el ángulo es positivo para los virajes hacia la izquierda y negativo para los virajes hacia la derecha.

Figura 2.7.m

Ángulos del observador del avión en el plano normal a la trayectoria del vuelo

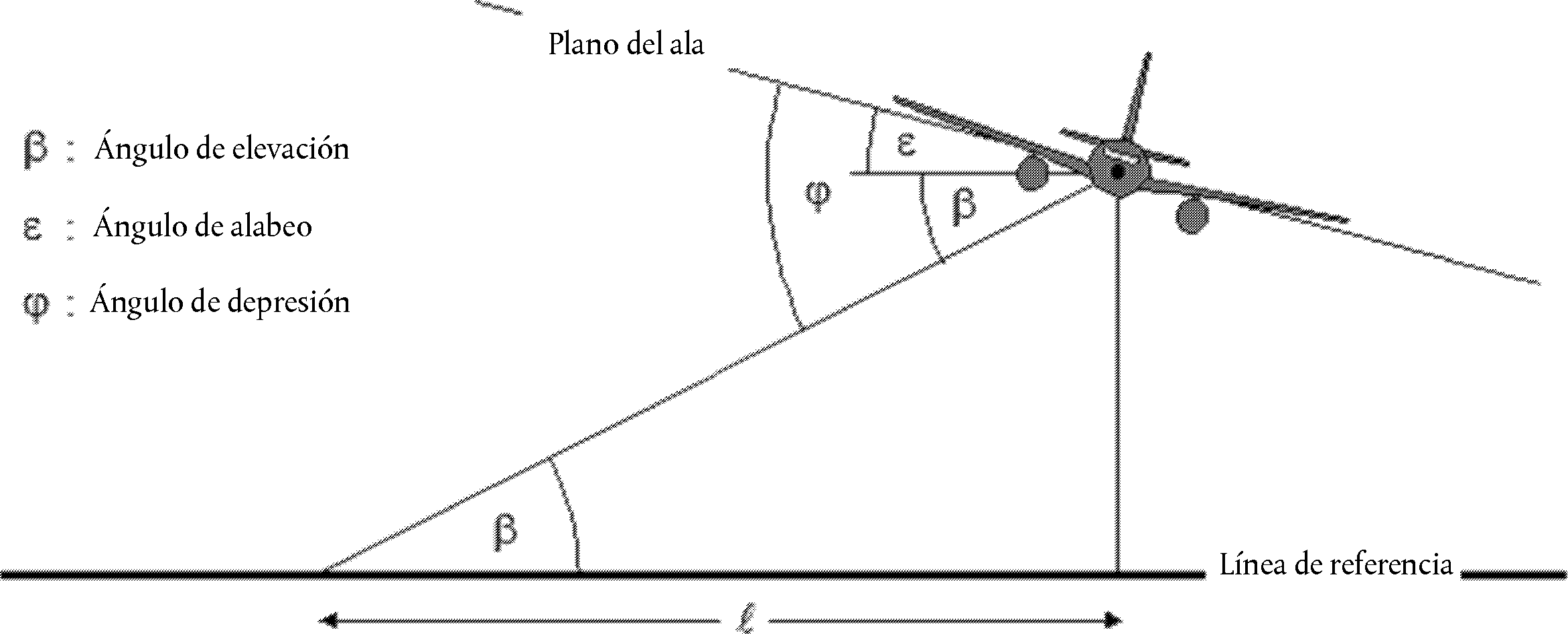
‒ El ángulo de elevación β (entre 0 y 90°) entre la trayectoria de la propagación sonora directa y la línea de tierra nivelada²³ determina, junto con la inclinación de la trayectoria del vuelo y el desplazamiento lateral ℓ del observador a partir de la trayectoria en tierra, la atenuación lateral.

²³ Si se trata de terreno no llano, pueden darse definiciones diferentes del ángulo de elevación. En este caso, se define mediante una altura del avión superior al punto de observación y a la distancia oblicua, de tal forma que se ignoren las pendientes del terreno local y los obstáculos de la trayectoria de propagación sonora (véanse las secciones 2.7.6 y 2.7.10). En el caso de que, debido a la elevación del terreno, el punto del receptor esté por encima del avión, el ángulo de elevación β resulta igual a cero.

‒ El ángulo de depresión φ entre el plano del ala y la trayectoria de propagación determina los efectos de la instalación del motor. Con respecto a la convención del ángulo de alabeo φ = β ± ε con el signo positivo para los observadores a estribor (derecha) y negativo para los observadores a babor (izquierda).

Corrección de la instalación del motor ΔI.

Un avión en vuelo es una fuente sonora compleja. No solo son las fuentes del motor (y el fuselaje) complejos en el origen, sino también la configuración del fuselaje, en particular la ubicación de los motores, las influencias de los patrones de radiación sonora a través de procesos de reflexión, refracción y difusión mediante superficies sólidas y campos de flujo aerodinámico. Esto tiene como consecuencia una direccionalidad no uniforme del sonido irradiado lateralmente sobre el eje de balanceo del avión, que en este contexto se denomina directividad lateral.

Hay diferencias importantes en la directividad lateral entre el avión con motores montados en fuselaje y en la parte inferior de las alas, y se prevén en la siguiente expresión:

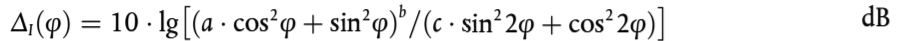
(2.7.37)

donde Δ_I(φ) es la corrección, en dB, para el ángulo de depresión φ (véase la figura 2.7.m) y

a = 0,00384, b = 0,0621, c = 0,8786 para motores montados en las alas;

a = 0,1225, b = 0,3290, c = 1 para motores montados en fuselaje.

En el caso de los aviones con hélice, las variaciones de directividad son insignificantes y, por esto, se puede suponer que:

Δ_I(φ) = 0

(2.7.38)

En la figura 2.7.n se muestra la variación de Δ_I(φ) sobre el eje de balanceo del avión para las tres instalaciones del motor. Estas relaciones empíricas las ha obtenido la SAE a partir de mediciones empíricas realizadas principalmente debajo del ala. Hasta que se hayan analizado los datos del ala superior, se recomienda que, para φ negativo, Δ_I(φ) = Δ_I(0) para todas las instalaciones.

Figura 2.7.n

Directividad lateral de los efectos de la instalación

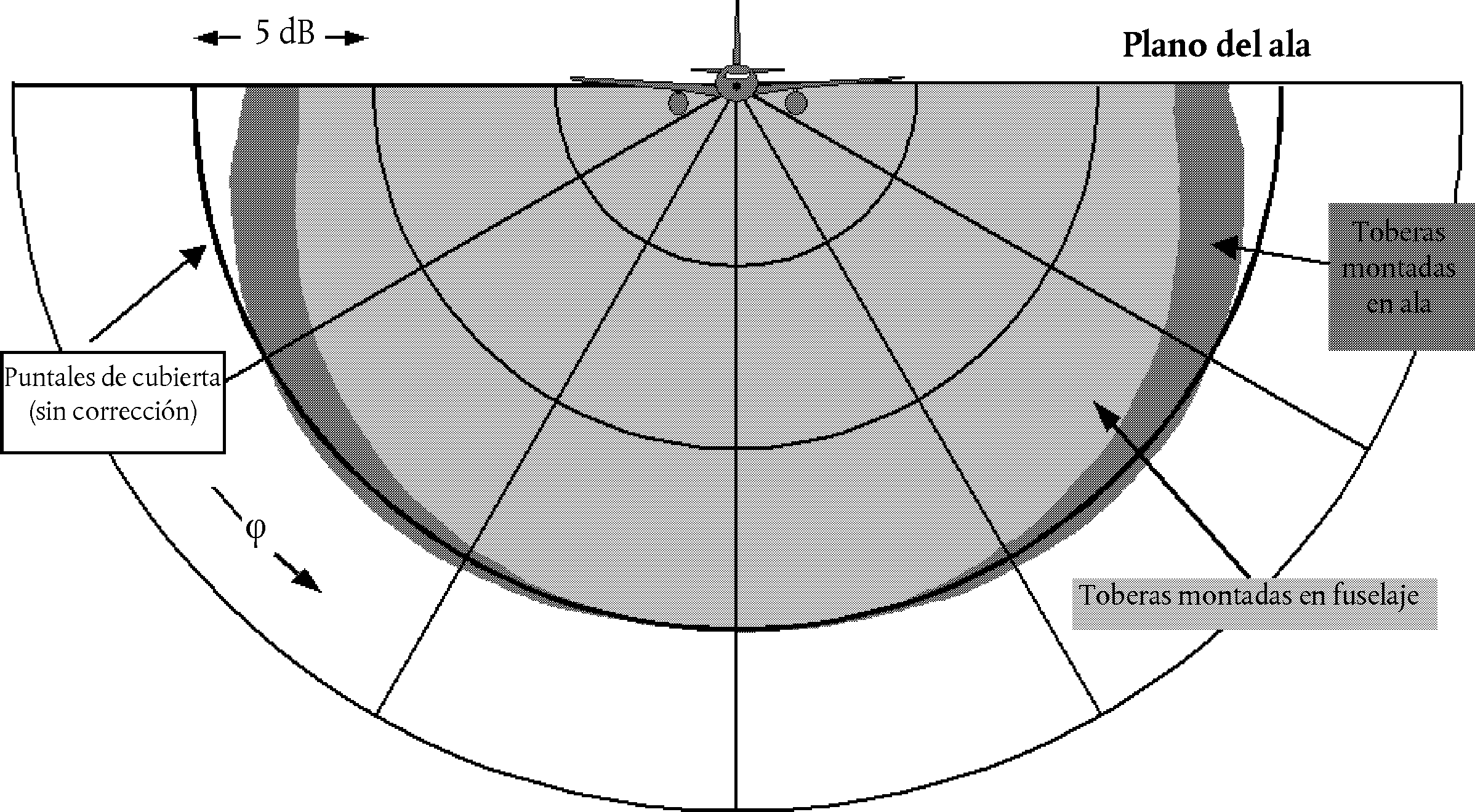
Se supone que Δ_I(φ) es bidimensional; es decir, no depende de ningún otro parámetro, y en particular que no varía con la distancia longitudinal al observador del avión. Esto significa que el ángulo de elevación β para Δ_I(φ) se define como β = tan^–1(z/ℓ).

Esto se adopta para facilitar la modelización hasta que se conozcan mejor los mecanismos; en realidad, los efectos de la instalación están obligados a ser sustancialmente tridimensionales. A pesar de ello, se justifica un modelo bidimensional por el hecho de que los niveles del evento tienden a estar dominados por el ruido radiado hacia los lados desde el segmento más próximo.

Atenuación lateral Λ(β, ℓ) (trayectoria de vuelo infinita).

Los niveles de eventos NPD tabulados están relacionados con un vuelo nivelado uniforme y, por lo general, se basan en mediciones realizadas a 1,2 m sobre el nivel de un terreno blando debajo del avión; el parámetro de la distancia se desarrolla efectivamente por encima de la superficie del terreno. Se supone que los efectos de la superficie en los niveles de ruido del evento debajo del avión, que pueden dar lugar a que los niveles tabulados difieran de los valores de campo libre²⁴, son inherentes a los datos (es decir, en el perfil de las curvas nivel de ruido –distancia).

²⁴ Un nivel de «campo libre» es el que se observaría si la superficie de tierra no estuviera ahí.

En los lados de la trayectoria del vuelo, el parámetro de la distancia es la distancia oblicua mínima ‒la longitud de la normal desde el receptor hasta la trayectoria del vuelo‒. En cualquier posición, el nivel de ruido por lo general será inferior a la misma distancia inmediatamente debajo del avión. Aparte de la directividad lateral o de los efectos de la instalación descritos anteriormente, una atenuación lateral excesiva da lugar a que el nivel de sonido disminuya con más rapidez con la distancia en comparación con lo que indican las curvas NPD. La Sociedad de Ingenieros Técnicos en Automoción (SAE) desarrolló un método que anteriormente se utilizaba ampliamente para la modelización de la propagación lateral del ruido del avión en AIR-1751 y los algoritmos descritos a continuación se basan en las mejoras de AIR-5662 que actualmente recomienda la SAE. La atenuación lateral es un efecto de reflexión, debido a la interferencia entre el sonido directamente radiado y que se refleja desde la superficie. Depende de la naturaleza de la superficie y puede causar reducciones significativas de los niveles de sonido observados para ángulos de elevación bajos. También se ve fuertemente afectada por la refracción del sonido, uniforme o no uniforme, causada por las turbulencias y los gradientes de viento y temperatura que se atribuyen a la presencia de la superficie²⁵. El mecanismo de la reflexión del terreno se conoce bastante bien y, para condiciones de la superficie y atmosféricas uniformes, en teoría se puede describir con cierta precisión. No obstante, la falta de uniformidades de la superficie y de las condiciones atmosféricas ‒que no son susceptibles de análisis teóricos sencillos‒ tienen un efecto profundo en el efecto de reflexión, de manera que tiende a «extenderlo» a ángulos de elevación más altos; por tanto, la teoría es de aplicabilidad limitada. SAE continua trabajando para comprender mejor los efectos de la superficie, y se espera que ello derive en modelos mejorados. Hasta lograrlo, se recomienda la siguiente metodología, descrita en AIR-5662, para calcular la atenuación lateral. Se limita al caso de la propagación sonora sobre una superficie nivelada blanda que resulta apropiada para la mayoría de los aeropuertos civiles. Aún se están desarrollando los ajustes para tener en cuenta una superficie del terreno dura (o, lo que es lo mismo en términos acústicos, el agua).

²⁵ Las turbulencias y los gradientes de temperatura y viento dependen en cierta medida de las características de la rugosidad y la transferencia térmica de la superficie.

La metodología se basa en datos experimentales sobre la propagación sonora desde una aeronave con motores montados en el fuselaje en un vuelo nivelado, constante y recto (sin virajes) registrado inicialmente en AIR-1751. Suponiendo que, para vuelos nivelados, la atenuación aire-tierra depende del i) ángulo de elevación β medido en el plano vertical y del ii) desplazamiento lateral con respecto a la trayectoria en tierra del avión ℓ, los datos se analizaron para obtener una función empírica para el ajuste lateral total Λ_T(β, ℓ) (= nivel del evento lateral menos el nivel a la misma distancia debajo del avión).

Como el término Λ_T(β, ℓ) representaba la directividad lateral y la atenuación lateral, la última puede extraerse mediante sustracción. Describiendo la directividad lateral mediante la ecuación 2.7.37, con coeficientes establecidos para jets montados en fuselaje y con φ reemplazado por β (apropiado para vuelos sin viraje), la atenuación lateral resulta:

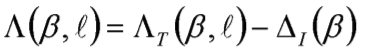
(2.7.39)

donde β y ℓ se miden tal y como se ilustra en la figura 2.7.m en un plano normal a la trayectoria de vuelo infinita que, para vuelos nivelados, también es vertical.

Aunque Λ(β,ℓ) podría calcularse directamente mediante la ecuación 2.7.39 con Λ_T(β,ℓ) obtenido de AIR-1751, se recomienda una relación más eficiente. Se trata de la siguiente aproximación empírica adaptada desde AIR-5662:

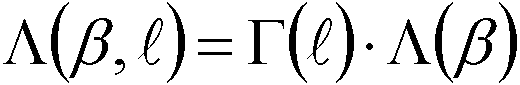
(2.7.40)

donde Γ(ℓ) es un factor de distancia obtenido mediante:

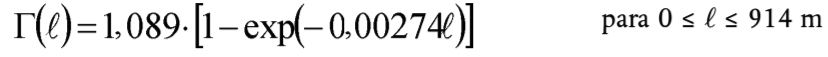
(2.7.41)

(2.7.42)

y Λ(β) es la atenuación lateral aire-tierra de larga distancia calculada mediante

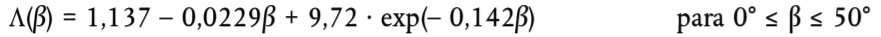
(2.7.43)

(2.7.44)

La expresión para la atenuación lateral Λ(β,ℓ), la ecuación 2.7.40, que se supone que se ajusta bien para todos los aviones, aviones con hélice y aviones con montaje en fuselaje y en alas, se ilustra gráficamente en la figura 2.7.o.

En determinadas circunstancias (con terreno), es posible que β sea menor que cero. En tales casos, se recomienda que Λ(β) = 10,57.

Figura 2.7.o

Variación de la atenuación lateral Λ(β,ℓ) con la distancia y el ángulo de elevación

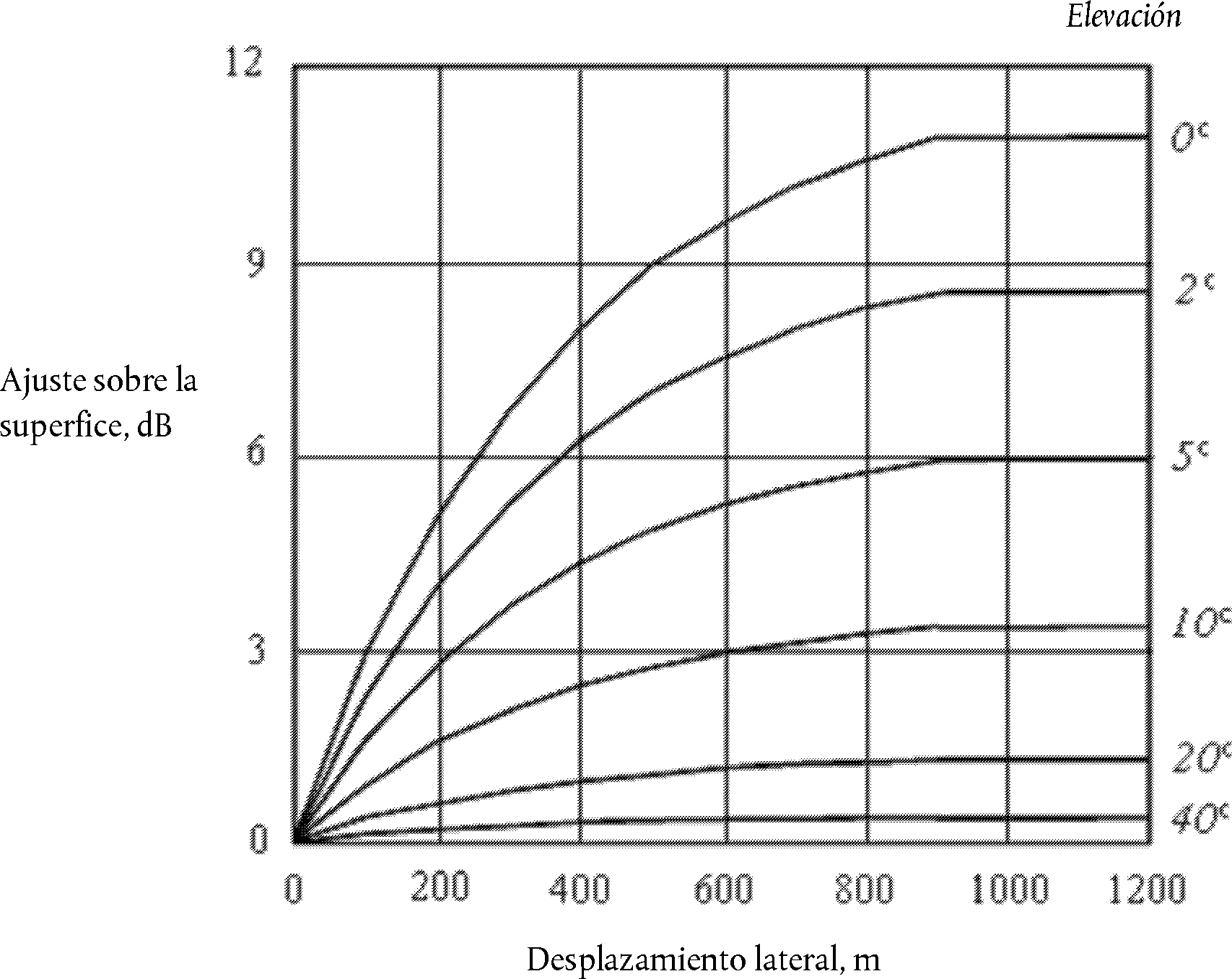
Atenuación lateral de segmentos finitos.

Las ecuaciones 2.7.41 a 2.7.44 describen la atenuación lateral Λ(β,ℓ) del sonido que llega al observador desde el avión en un vuelo uniforme a lo largo de una trayectoria de vuelo nivelada e infinita Al aplicarlas a segmentos de trayectoria finitos que no están nivelados, la atenuación debe calcularse para una trayectoria nivelada equivalente ‒ya que el punto más próximo de una extensión simple del segmento inclinado (que pasa a través de la superficie de tierra en un determinado punto) normalmente no ofrece un ángulo de elevación apropiado β.

La determinación de la atenuación lateral para segmentos finitos difiere significativamente para los índices L_max y L_E. Los niveles máximos del segmento L_max se determinan a partir de los datos NPD como una función de la distancia de propagación d a partir del punto más próximo del segmento; no es preciso realizar correcciones para tener en cuenta las dimensiones del segmento. Asimismo, se supone que la atenuación lateral L_max depende solo del ángulo de elevación del mismo punto y también de la distancia de terreno. Por tanto, solo se necesitan las coordenadas de dicho punto. Pero para L_E, el proceso es más complicado.

El nivel del evento básico L_E(P,d) determinado a partir de los datos NPD, incluso para parámetros de segmentos finitos, se refiere a una trayectoria de vuelo infinita. Evidentemente, el nivel de exposición sonora del evento, L_E,seg, es evidentemente inferior al nivel básico ‒debido a la corrección del segmento finito definida más adelante en la sección 2.7.19‒. Dicha corrección, una función de la geometría de triángulos OS₁S₂ tal y como se refleja en las figuras 2.7.j a 2.7.l, define qué proporción de la energía sonora total de la trayectoria infinita recibida en O procede del segmento; se aplica la misma corrección, independientemente de que haya o no alguna atenuación lateral. Pero todas las atenuaciones laterales deben calcularse para la trayectoria de vuelo infinita, es decir, como una función de su desplazamiento y su elevación, pero no para el segmento finito.

Sumando las correcciones Δ_V y Δ_I, y restando la atenuación lateral Λ(β,ℓ) al nivel básico NPD se obtiene el nivel de ruido del evento ajustado para un vuelo nivelado uniforme equivalente sobre una trayectoria recta infinita adyacente. No obstante, los segmentos de la trayectoria de vuelo real modelizados, los que afectan a las curvas de nivel de ruido, rara vez están nivelados; el avión suele ascender o descender.

En la figura 2.7.p se ilustra un segmento de salida S₁S₂ ‒el avión asciende a un ángulo γ‒, pero las consideraciones son muy similares para una llegada. No se muestra el resto de la trayectoria de vuelo «real»; basta con destacar que S₁S₂ representa solo una parte de toda la trayectoria (que por lo general será curvada). En este caso, el observador O están a un lado del segmento y a su izquierda. El avión experimenta un movimiento de alabeo (movimiento en sentido contrario a las agujas del reloj sobre la trayectoria del vuelo) a un ángulo ε en el eje horizontal lateral. El ángulo de depresión φ desde el plano del ala, del que el efecto de la instalación Δ_I es una función (ecuación 2.7.39), se encuentra en el plano normal de la trayectoria del vuelo en que se define ε. Por tanto, φ = β – ε, donde β = tan^–1(h/ℓ) y ℓ es la distancia perpendicular OR desde el observador hasta la trayectoria en tierra; es decir, el desplazamiento lateral del observador²⁶. El punto de aproximación más cercano del avión al observador, S, se define mediante la perpendicular OS, de longitud (distancia oblicua) d_p. El triángulo OS₁S₂ se atiene a la ilustración de la figura 2.7.k, la geometría para calcular la corrección del segmento Δ_F.

²⁶ Si se trata de un observador ubicado en el lateral derecho del segmento φ resultaría β + ε (véase la sección 2.7.19).

Figura 2.7.p

Observador a un lado del segmento

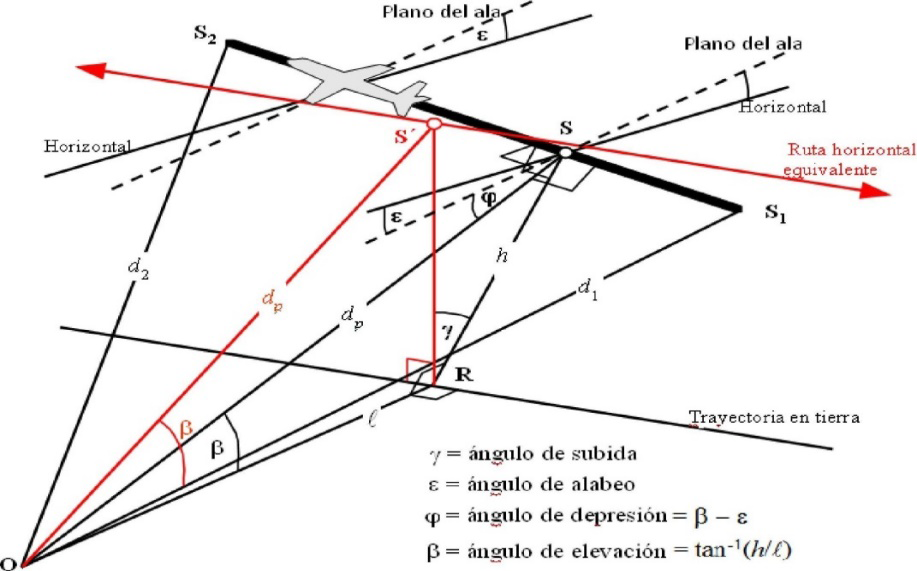
Para calcular la atenuación lateral mediante la ecuación 2.7.40 (donde β se mide en un plano vertical), una trayectoria de vuelo nivelado equivalente se define en el plano vertical a través de S₁S₂ y con la misma distancia oblicua perpendicular d_p desde el observador. Esto se visualiza rotando el triángulo ORS, y su trayectoria de vuelo relacionada, sobre OR (véase la figura 2.7.p) girándolo un ángulo γ, formando así el triángulo ORS′. El ángulo de elevación de esta trayectoria nivelada equivalente (ahora en un plano vertical) es β = tan^–1(h/ℓ) (ℓ permanece invariable). En este caso, con el observador al lado, la atenuación lateral Λ(β,ℓ) es la misma para los índices L_E y L_max.

En la figura 2.7.q se ilustra la situación cuando el punto del observador O se encuentra detrás del segmento finito, y no en un lado. En este caso, el segmento se observa como un tramo más distante de una trayectoria infinita; solo se puede dibujar una perpendicular hasta el punto S_p sobre su extensión. El triángulo OS₁S₂ se atiene a lo que se ilustra en la figura 2.7.j que define la corrección del segmento Δ_F. No obstante, en este caso, los parámetros de la directividad lateral y de la atenuación son menos evidentes.

Figura 2.7.q

Observador detrás del segmento

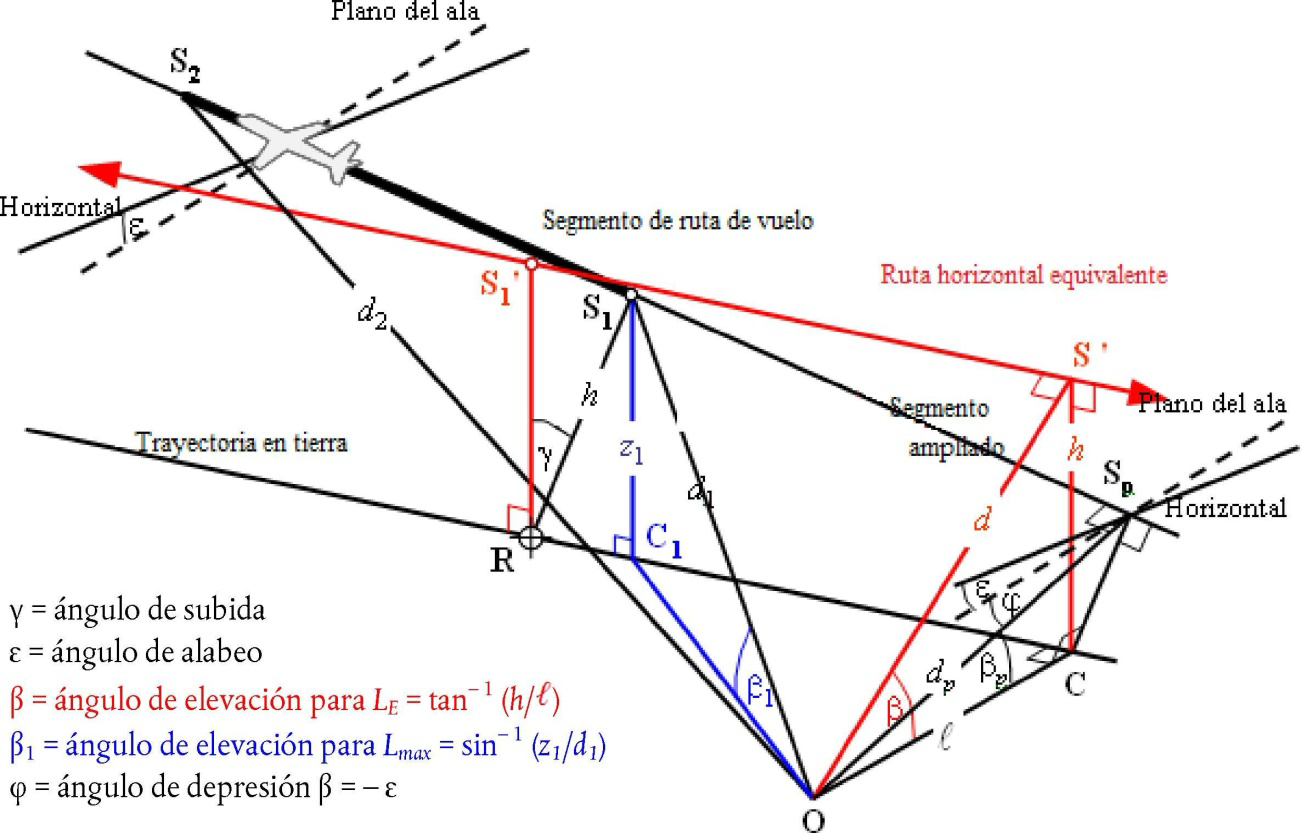
Conviene recordar que, considerada a efectos de modelización, la directividad lateral (efecto de la instalación) es bidimensional, el ángulo de depresión definido φ se mide en lateral a partir del plano del ala del avión. (El nivel del evento básico es el que resulta de la travesía del avión por la trayectoria de vuelo infinita representada mediante el segmento ampliado). De esta forma, se determina el ángulo de depresión en el punto de aproximación más cercano, es decir, φ = β_p – ε donde β_p es el ángulo S_pOC.

Para índices de nivel máximo, el parámetro de distancia NPD se considera como la distancia más corta hasta el segmento, es decir, d = d₁. Para índices del nivel de exposición, se trata de la distancia más corta d_p de O a S_p sobre la trayectoria de vuelo ampliada; es decir, el nivel interpolado a partir de las tablas NPD es L_E∞(P₁,d_p).

Los parámetros geométricos para la atenuación lateral también difieren para los cálculos del nivel máximo y de exposición.

Para índices del nivel máximo, el ajuste Λ(β,ℓ) resulta de la ecuación 2.7.40 con β = β₁ = sin^{– 1}(z₁/d₁) y 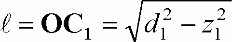, donde β₁ y d₁ se definen mediante el triángulo OC₁S₁ en el plano vertical a través de O y S₁.

Al calcular la atenuación lateral de los segmentos aéreos solamente y el índice del nivel de exposición, ℓ es el desplazamiento lateral más corto desde la extensión del segmento (OC). No obstante, para definir un valor apropiado de β, una vez más resulta necesario visualizar una trayectoria de vuelo nivelada equivalente (infinita), en la que el segmento se pueda considerar como una parte integrante. Se dibuja a través de S₁′, con una altura h por encima de la superficie, donde h es igual a la longitud de RS₁, la perpendicular desde la trayectoria en tierra hasta el segmento. Esto equivale a la rotación de la trayectoria de vuelo real ampliada girándola un ángulo γ sobre el punto R (véase la figura 2.7.q). En la medida en que R se encuentre en la perpendicular a S₁, el punto del segmento más próximo a O, la construcción de la trayectoria nivelada equivalente es la misma cuando O está a un lado del segmento.

El punto de aproximación más cercano de la trayectoria nivelada equivalente al observador O se encuentra en S′, con una distancia oblicua d, de tal forma que el triángulo OCS′ formado en el plano vertical defina el ángulo de elevación β = cos^–1(ℓ/d). Aunque esta transformación parece ser bastante enrevesada, cabe destacar que la geometría de la fuente básica (definida mediante d₁, d₂ y φ) permanece inalterada, el sonido que viaja desde el segmento hacia el observador es simplemente el que sería si todo el vuelo a través del segmento inclinado con una extensión infinita (del que forma parte el segmento a efectos de modelización) se realizara a una velocidad constante V y con una potencia P₁. La atenuación lateral del sonido desde el segmento recibida por el observador, por otra parte, no está relacionada con el ángulo de elevación β_p, de la trayectoria ampliada, sino con β, de la trayectoria nivelada equivalente.

El caso de un observador delante del segmento no se describe por separado; es evidente que se trata básicamente del mismo caso que cuando el observador está detrás.

No obstante, para los índices del nivel de exposición en que las ubicaciones del observador están detrás de los segmentos en tierra durante el rodaje antes del despegue y las ubicaciones que están delante de los segmentos en tierra durante el rodaje después del aterrizaje, el valor de β resulta ser el mismo que para los índices de nivel máximo, es decir, β = β 1 = sin^–1(z₁/d₁) y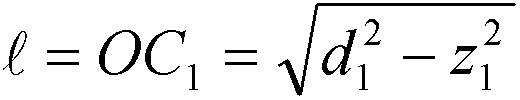

Corrección de segmentos finitos Δ_F (solo para niveles de exposición L_E).

El nivel de exposición al ruido básico ajustado está relacionado con un avión que sigue un vuelo nivelado uniforme, recto y constante (aunque con un ángulo de alabeo ε que está en consonancia con un vuelo recto). Con la aplicación de la corrección del segmento finito (negativa) Δ_F = 10×lg(F), donde F es la fracción de energía, se ajusta aún más el nivel que se conseguiría si el avión recorriera solo el segmento finito (o si fuera totalmente silencioso para el resto de la trayectoria de vuelo infinita).

El término «fracción de energía» tiene en cuenta la directividad longitudinal pronunciada del ruido de un avión y el ángulo subtendido por el segmento en la posición del observador. A pesar de que los procesos que causan la direccionalidad son muy complejos, los estudios han revelado que las curvas de nivel de ruido resultantes son bastante poco sensibles a las características direccionales precisas asumidas. La expresión de Δ_F que se indica a continuación se basa en un modelo dipolar de 90 grados de potencia cuarta.

Se supone que no se ve afectado por la directividad lateral ni por la atenuación. La forma en que se halla la corrección se describe detalladamente en el apéndice E.

La fracción de energía F es una función de la «vista» de triángulo OS₁S₂ definida en las figuras 2.7.j a 2.7.l, como:

(2.7.45)

Con

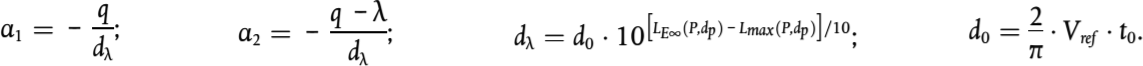
donde dλ se considera como la «distancia a escala» (véase el apéndice E). Tenga en cuenta que L_max(P, d_p) es el nivel máximo, a partir de los datos de NPD, para la distancia perpendicular d_p, NO el segmento L_max.

Es aconsejable aplicar un límite inferior de ‒ 150 dB a Δ_F.

En el caso particular de que las ubicaciones del observador se encuentren detrás de cada segmento de rodaje de desplazamiento en tierra antes del despegue y de cada segmento de desplazamiento en tierra firme en el aterrizaje, se usa una forma reducida de la fracción del ruido expresada en la ecuación 2.7.45, que se corresponde con el caso específico de q = 0. Esto se calcula como sigue:

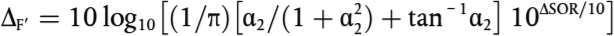
(2.7.46)

donde α2 = λ/dλ y Δ_SOR es la función de la directividad del punto de partida de rodaje definida por las ecuaciones 2.7.51 y 2.7.52.

El planteamiento para utilizar esta forma particular de la fracción de ruido se explica más a fondo en la siguiente sección, como parte del método de la aplicación de la directividad del punto de partida de rodaje.

Tratamientos específicos de los segmentos de desplazamientos en tierra, incluida la función de la directividad del punto de partida de rodaje Δ_SOR.

En el caso de los segmentos de desplazamiento en tierra firme, tanto para el despegue como para el aterrizaje, se aplican tratamientos específicos, que se describen a continuación.

Función de la directividad de inicio de rodaje Δ_SOR.

El ruido del reactor ‒en particular los equipados con motores con una relación de derivación inferior‒ muestra un modelo de radiación lobulada en el arco posterior, que es característico del ruido de escape del reactor. Este modelo es más importante cuanto más alta sea la velocidad del reactor y más baja sea la velocidad del avión. Esto reviste una importancia particular para las ubicaciones del observador detrás del punto de partida de rodaje, cuando se cumplan ambas condiciones. Este efecto se tiene en cuenta mediante una función de directividad Δ_SOR.

La función Δ_SOR se ha calculado a partir de varias campañas de mediciones de ruido mediante la utilización de micrófonos correctamente colocados detrás y en el lateral del punto de partida de rodaje del reactor que se dispone a salir.

En la figura 2.7.r se ilustra la geometría pertinente. El ángulo de azimut ψ entre el eje longitudinal del avión y el vector para el observador se define como sigue:

(2.7.47)

La distancia relativa q es negativa (véase la figura 2.7.j), de tal forma que los intervalos ψ desde 0° en la dirección del avión que sigue su rumbo hasta 180º en la dirección inversa.

Figura 2.7.r

Geometría en tierra del observador del avión para la estimación de la corrección de la directividad

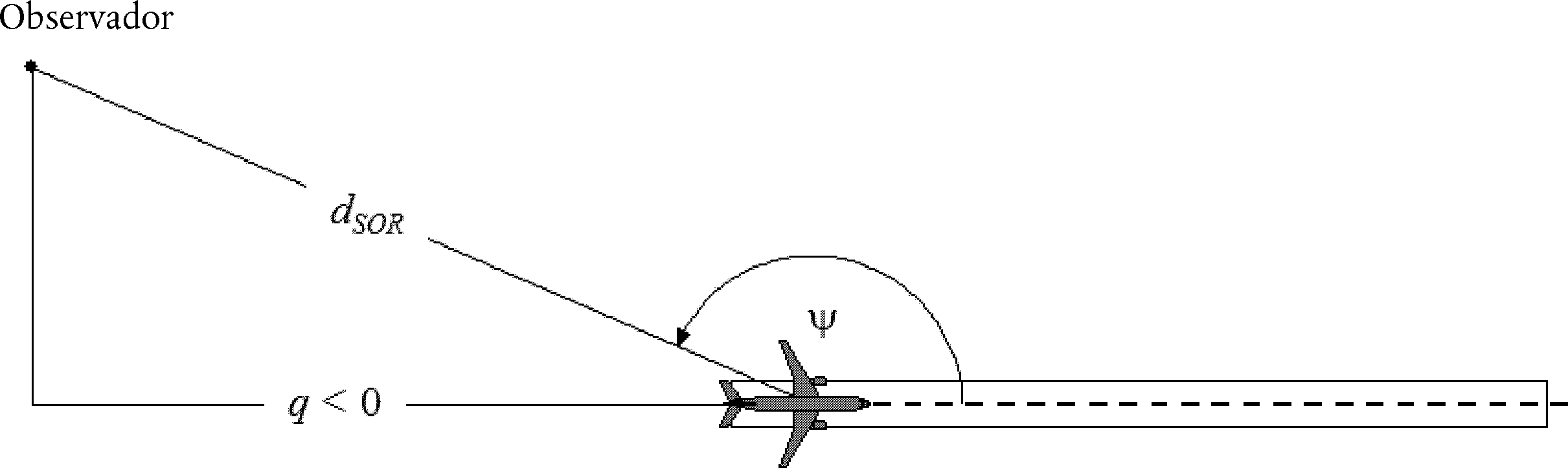
La función Δ_SOR representa la variación del ruido total que produce el desplazamiento en tierra firme antes del despegue medido detrás el punto de partida de rodaje, en relación con el ruido total del desplazamiento en tierra firme antes del despegue medido en el lateral del punto de partida de rodaje, a la misma distancia:

L_TGR(d_SOR,ψ) = L_TGR(d_SOR,90°) + Δ_SOR(d_SOR,ψ)

(2.7.48)

donde L_TGR(d_SOR,90°) es el nivel de ruido general del desplazamiento en tierra firme antes del despegue que generan todos los segmentos del desplazamiento en tierra firme antes del despegue a la distancia puntual d_SOR en el lateral del punto de partida de rodaje. A distancias d_SOR inferiores a la distancia normalizada d_SOR,0, la función de la directividad del punto de partida de rodaje se obtiene de:

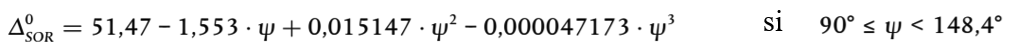
(2.7.49)

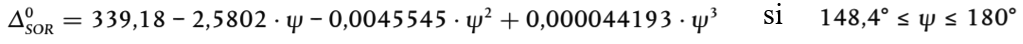
(2.7.50)

Si la distancia d_SOR excede la distancia de normalización d_SOR,0, la corrección de la directividad se multiplica mediante un factor de corrección para tener en cuenta el hecho de que la directividad reviste menor importancia para distancias más largas del avión, es decir:

(2.7.51)

(2.7.52)

La distancia de normalización d_SOR,0 es igual a 762 m (2 500 ft).

Tratamiento de los receptores ubicados detrás del segmento de desplazamiento en tierra firme en el despegue y en el aterrizaje.

La función Δ_SOR descrita anteriormente captura en gran medida el efecto de la directividad pronunciada del tramo inicial del rodaje en el despegue en ubicaciones por detrás del inicio de rodaje (porque se trata del punto más próximo a los receptores, con la máxima velocidad del reactor con respecto a la relación de transmisión del avión). No obstante, el uso de Δ_SOR establecido se «generaliza» para las posiciones detrás de cada segmento individual de desplazamiento en tierra firme, tanto para el despegue como para el aterrizaje, de tal manera que no solo se tiene en cuenta detrás del punto de inicio de rodaje (en el caso del despegue).

Los parámetros d_S y ψ se calculan en relación con el inicio de cada segmento individual de desplazamiento en tierra firme.

El nivel del evento L_seg para una ubicación por detrás de un segmento de desplazamiento en tierra firme al despegar o aterrizar se calcula para cumplir con los formalismos de la función Δ_SOR: básicamente se calcula para el punto de referencia ubicado en el lateral del punto inicial del segmento, a la misma distancia d_S que el punto real, y se ajusta aún más a Δ_SOR para obtener el nivel del evento en el punto real.

Esto significa que los diferentes términos de corrección de las ecuaciones siguientes deben usar los parámetros geométricos correspondientes a este punto de referencia ubicado en el lateral del punto inicial:

L_max,seg = L_max(P,d = d_s) + Δ_I(φ) – Λ(β,l = d_s) + Δ_SOR

(2.7.53)

L_E,seg = L_E,∞(P,d = d_s) + Δ_V + Δ_I(φ) – Λ(β,l = d_s) + Δ′_F + Δ_SOR

(2.7.54)

donde Δ′_F es la forma reducida de la fracción de ruido expresada en la ecuación q = 0 (ya que el punto de referencia se encuentra en el lateral del punto inicial) y recordando que dλ debe calcularse usando d_S (y no d_p):

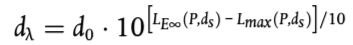
(2.7.55)

2.7.20. Nivel de ruido de un evento L del movimiento de una aeronave de la aviación general.

El método descrito en la sección 2.7.19 es aplicable a aeronaves de aviación general con motores de propulsión cuando se tratan como aviones de este tipo con respecto a los efectos de la instalación del motor.

La base de datos ANP incluye entradas de aeronaves de varias aeronaves de aviación general. Si bien se trata del funcionamiento más común de la aeronave de la aviación general, pueden darse ocasiones en que resulte conveniente usar datos adicionales.

Si la aeronave de la aviación general específica no se conoce o no se encuentra en la base de datos de ANP, se recomienda usar los datos más genéricos de la aeronave, GASEPF y GASEPV, respectivamente. Estos conjuntos de datos representan una aeronave pequeña de aviación general de un único motor con hélices de paso fijo y hélices de paso variable, respectivamente. Los cuadros de las entradas se presentan en el anexo I (cuadros I-11, I-17)

2.7.21. Método para calcular el ruido de los helicópteros.

Para calcular el ruido de los helicópteros, se puede usar el mismo método de cálculo utilizado para los aviones de ala fija (descrito en la sección 2.7.14), siempre que los helicópteros se consideren como aviones con hélices y que no se apliquen los efectos de la instalación del motor asociados con reactores. Los cuadros de las entradas para dos conjuntos de datos diferentes se presentan en el anexo I (cuadros I-18, I-27).

2.7.22. Ruido asociado con operaciones de pruebas del motor (prueba en tierra para control), rodaje y unidades de potencia auxiliares.

En tales casos en que se considere que el ruido asociado con las pruebas del motor y las unidades de potencia auxiliares se van a modelizar, la modelización se realiza según las indicaciones del capítulo dedicado al ruido industrial. Aunque no suele ser el caso, el ruido de las pruebas del motor del avión (lo que a veces se denomina «prueba de motor a punto fijo») en los aeropuertos puede contribuir a los impactos del ruido. Estas pruebas suelen realizarse a efectos de ingeniería para comprobar el rendimiento del motor, para lo que se colocan los aviones en zonas seguras lejos de los edificios y de los movimientos de aviones, vehículos y personal, a fin de evitar daños originados por el chorro del reactor.

Por motivos adicionales para el control de la seguridad y del ruido, los aeropuertos, en particular los que disponen de instalaciones de mantenimiento que pueden conllevar frecuentes ensayos de motores, pueden instalar las denominadas «pantallas antirruido», es decir, recintos dotados con deflectores en tres lados especialmente diseñadas para desviar y disipar el ruido y el chorro de los gases de combustión. La investigación del impacto del ruido de tales instalaciones, que se puede atenuar y reducir mediante el uso de muros de tierra o barreras acústicas, resulta más sencilla si se trata el recinto de pruebas como una fuente de ruido industrial y si se usa un modelo apropiado de propagación sonora.

2.7.23. Cálculo de los niveles acumulados.

En las secciones 2.7.14 a 2.7.19 se describe el cálculo del nivel de ruido del evento de un movimiento de un avión en una única ubicación del observador. La exposición al ruido total en dicha ubicación se calcula mediante la suma de los niveles del evento de todos los movimientos del avión significativos desde el punto de vista del ruido, es decir, todos los movimientos, entrantes y salientes, que influyen en el nivel acumulado.

2.7.24. Niveles sonoros continuos equivalentes ponderados.

Los niveles sonoros continuos equivalentes ponderados en el tiempo, que tienen en cuenta toda la energía sonora del avión recibida, deben expresarse de manera genérica mediante la fórmula:

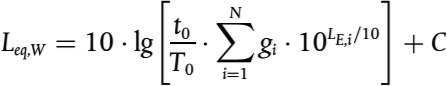
(2.7.56)

La suma se realiza para todos los eventos sonoros N durante el intervalo de tiempo al que se aplica el índice de ruido. L_E,i es el nivel de exposición al ruido de evento simple del evento acústico i, g_i es un factor de ponderación que depende del periodo del día (que suele definirse para los períodos del día, la tarde y la noche). Efectivamente, g_i es un multiplicador del número de vuelos que se producen durante los períodos específicos. La constante C puede tener significados diferentes (constante de normalización, ajuste estacional, etc.).

Usando la relación

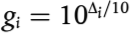
donde Δ_i es la ponderación en decibelios para el período i; se puede volver a definir la ecuación 2.7.56 como:

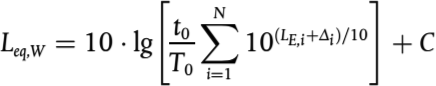
(2.7.57)

es decir, la consideración del día se expresa mediante un incremento adicional del nivel.

2.7.25. Número ponderado de operaciones.

El nivel de ruido acumulado se calcula mediante la suma de las contribuciones de todos los tipos o las categorías diferentes de aviones usando las diferentes rutas aéreas que conforman el escenario del aeropuerto.

Para describir este proceso de suma, se introducen los siguientes subíndices:

i: índice del tipo o la categoría del avión.

j: índice de la trayectoria o subtrayectoria del vuelo (en caso de que se definan subtrayectorias).

k: índice del segmento de la trayectoria del vuelo.

Muchos índices de ruido ‒especialmente los niveles sonoros continuos equivalentes‒ incluyen en su propia definición factores de ponderación del periodo del día g_i (ecuaciones 2.7.56 y 2.7.57).

El proceso de suma puede simplificarse mediante la introducción de un «número ponderado de operaciones»

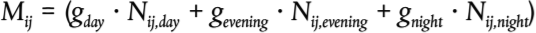
(2.7.58)

Los valores N_ij representan los números de operaciones del tipo o la categoría de avión i en la trayectoria (o subtrayectoria) j durante el día, la tarde y la noche, respectivamente²⁷.

²⁷ Los períodos de tiempo pueden diferir de estos tres, en función de la definición del índice de ruido utilizado.

A partir de la ecuación (2.7.57), el nivel d (genérico) el nivel sonoro continuo equivalente acumulativo L_eq en el punto de observación (x,y) es

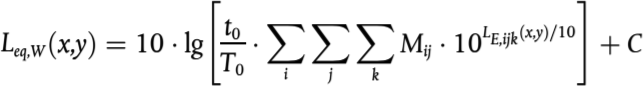
(2.7.59)

T₀ es el período de tiempo de referencia. Depende de la definición específica del índice ponderado utilizado (e.g. L_DEN), así como de los factores de ponderación (por ejemplo, L_DEN). L_E,ijk es la contribución del nivel de exposición al ruido de evento simple del segmento k de la trayectoria o subtrayectoria j para la operación de un avión de la categoría i. El cálculo de f L_E,ijk se describe de manera detallada en las secciones 2.7.14 a 2.7.19.

2.7.26. Cálculo y ajuste de una malla estándar.

Cuando las curvas de nivel de ruido (isófonas) se obtienen mediante la interpolación entre los valores del índice en los puntos de una malla en forma rectangular, su precisión depende de la elección de la separación de la cuadrícula (o del paso de la malla) Δ_G, en particular en el interior de las celdas en que los gradientes grandes de la distribución espacial de los valores del índice causan una fuerte curvatura de las isófonas (véase la figura 2.7.s). Los errores de interpolación se reducen disminuyendo el paso de malla, pero a medida que aumenta el número de puntos de la cuadrícula, también aumenta el tiempo de cálculo. La optimización de una malla de cuadrícula regular implica equilibrar la precisión de la modelización y el tiempo de ejecución.

Figura 2.7.s

Cuadrícula estándar y ajuste de la cuadrícula

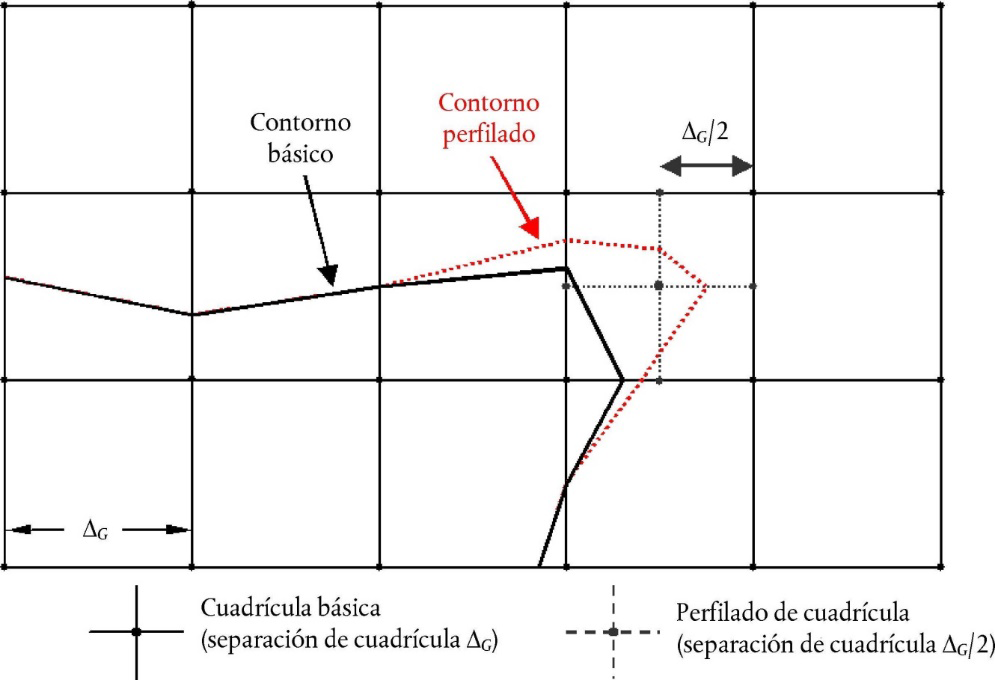
Una mejora importante en la eficacia del cálculo que ofrece resultados más precisos es utilizar una cuadrícula irregular para ajustar la interpolación en celdas importantes. La técnica, ilustrada en la figura 2.7.s, consiste en reforzar la malla localmente, dejando invariable la mayor parte de la cuadrícula. Se trata de una operación muy sencilla, que se consigue con los siguientes pasos:

1. Se define una diferencia del umbral de ajuste ΔL_R para el índice de ruido.

2. Se calcula la cuadrícula básica para una separación Δ_G.

3. Se comprueban las diferencias ΔL de los valores del índice entre los nudos adyacentes de la red.

4. Si hay alguna diferencia ΔL > ΔL_R, se define una nueva red con una separación Δ_G/2 y se calculan los niveles de los nuevos nudos de la siguiente forma:

5. Se repiten los pasos de 1 a 4 hasta que todas las diferencias sean menores que la diferencia del umbral.

6. Se calculan las isófonas mediante una interpolación lineal.

Si la matriz de los valores de índice se va a agregar a otras (por ejemplo, al calcular índices ponderados mediante la suma de curvas de nivel de ruido independientes del día, la tarde y la noche), es necesario proceder con precaución para garantizar que las redes independientes sean idénticas.

2.7.27. Uso de mallas rotadas.

En muchos casos prácticos, la forma real de las curvas de nivel de ruido tiende a ser simétrica respecto a la trayectoria en tierra. No obstante, si la dirección de esta trayectoria no está alineada con la malla de cálculo, esto puede dar lugar a una forma de isófona asimétrica.

Figura 2.7.t

Uso de una malla rotada

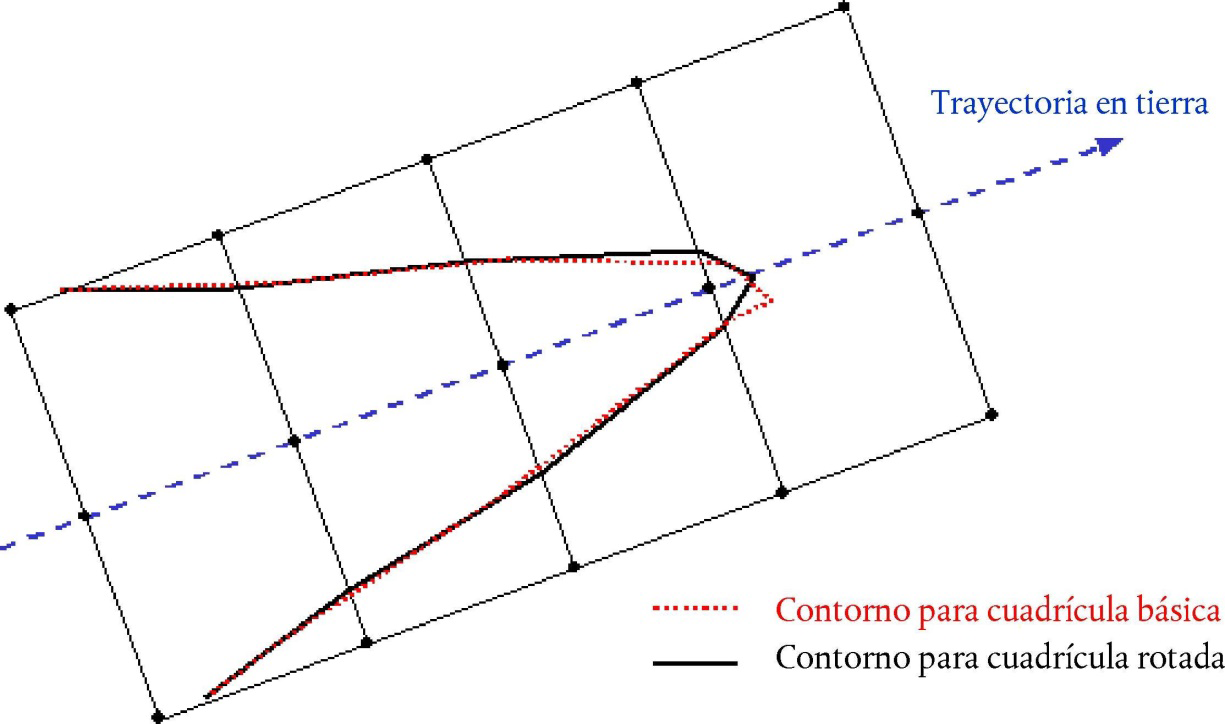
Una forma sencilla de evitar este efecto es incrementar los nodos de la malla. No obstante, esto aumenta el tiempo de cálculo. Una solución más elegante consiste en girar la cuadrícula de cálculo, de tal manera que su dirección sea paralela a las trayectorias en tierra principales (que suelen ser paralelas a la pista principal). En la figura 2.7.t se muestra el efecto de la rotación de la malla en la forma de la isófona.

2.7.28. Trazado de las curvas de nivel de ruido (isófonas).

Un algoritmo muy eficaz en términos de tiempo que elimina la necesidad de calcular la matriz de los valores de índice de una malla completa a expensas de un cálculo algo más complejo es trazar la línea de las curvas de nivel de ruido, punto por punto. Esta opción requiere que se apliquen y repitan dos pasos básicos (véase la figura 2.7.u):

Figura 2.7.u

Concepto de algoritmo trazador

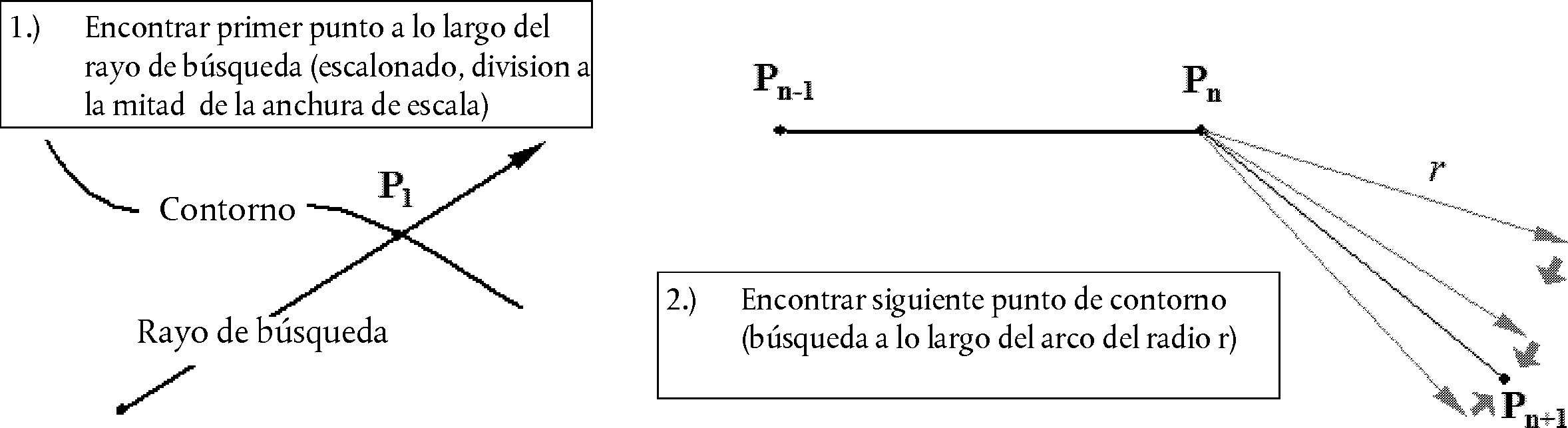
El paso 1 consiste en encontrar un primer punto P₁ de una determinada isófona. Para ello, se calculan los niveles del índice de ruido L en puntos equidistantes a lo largo del «rayo de búsqueda» que se espera que cruce esta isófona L_C. Cuando esta se cruza, la diferencia δ = L_C – L cambia de signo. Entonces, se divide a la mitad el ancho del paso a lo largo del rayo y se invierte la dirección de la búsqueda. Se repite el proceso hasta que δ es más pequeño que el umbral de precisión predefinido.

El paso 2, que se repite hasta que la curva de nivel de ruido está suficientemente bien definida, consiste en encontrar el próximo punto en el contorno L_C, que se encuentra a una distancia en línea recta específica r del punto actual. Se procede con pasos angulares consecutivo, calculándose los niveles de índice y las diferencias δ en los extremos de los vectores que describen un arco con radio r. De manera similar a la anterior, al reducir a la mitad e invertir los incrementos, en esta ocasión en las direcciones del vector, el próximo punto del contorno se determina conforme a una precisión predefinida.

Figura 2.7.v

Parámetros geométricos que definen las condiciones para el algoritmo trazador

Se deben imponer determinadas restricciones para garantizar que la curva de nivel de ruido se calcula con un grado suficiente de precisión (véase la figura 2.7.v):

1) La longitud de la cuerda Δc (la distancia entre los dos puntos de la curva de nivel de ruido) debe encuadrarse dentro de un intervalo [Δc_min, Δc_max], por ejemplo [10 m, 200 m].

2) La proporción de longitud entre las dos cuerdas adyacentes de longitudes Δc_n y Δc_{n + 1} debe limitarse, por ejemplo 0,5 < Δc_n / Δc_{n + 1} < 2.

3) Con respecto a un buen ajuste de la longitud de la cuerda a la curvatura de la isófona, se debe cumplir la siguiente condición:

Φ_n · max(Δc_n – 1, Δc_n) ≤ ε (ε≈ 15 m)

donde f_n es la diferencia en los rumbos de la cuerda.

La experiencia con este algoritmo ha revelado que, como promedio, entre dos y tres valores de índice deben calcularse para determinar un punto de la curva con una precisión superior a 0,01 dB.

Especialmente cuando se tienen que calcular curvas de nivel amplias, este algoritmo acelera significativamente el tiempo de cálculo. No obstante, cabe destacar que esta aplicación precisa de experiencia, sobre todo cuando una curva de nivel de ruido se divide en islas separadas.

2.8. Asignación de niveles de ruido y población a los edificios.

A efectos de evaluar la exposición de la población al ruido, solo se deben tener en cuenta los edificios residenciales. Por tanto, no se debe asignar ninguna persona a edificios que no sean para uso residencial, tales como colegios, hospitales, edificios para oficinas o fábricas. La asignación de la población a edificios residenciales debe basarse en los últimos datos oficiales (en función de los reglamentos correspondientes de los Estados miembros).

Habida cuenta de que el cálculo del ruido de las aeronaves se realiza para una cuadrícula con una resolución 100 m × 100 m, en el caso específico del ruido de aeronaves, los niveles deben interpolarse en función de los niveles de ruido de la malla de cálculo más próxima.

Determinación del número de habitantes de un edificio.

El número de habitantes de un edificio residencial es un parámetro intermedio importante para calcular la exposición al ruido. Lamentablemente, estos datos no siempre se encuentran disponibles. A continuación, se especifica cómo puede hallarse este parámetro a partir de datos que se encuentran disponibles con mayor frecuencia.

Los símbolos utilizados a continuación son:

BA = superficie en planta del edificio.

DFS = superficie residencial útil.

DUFS = superficie residencial útil de cada vivienda.

H = altura del edificio.

FSI = superficie de vivienda por habitante.

Inh = número de habitantes.

NF = número de plantas del edificio.

V = volumen de edificios residenciales.

Para calcular el número de habitantes, debe usarse el procedimiento del caso 1 siguiente o el del caso 2, en función de la disponibilidad de los datos.

CASO 1: se encuentran disponibles los datos sobre el número de habitantes.

1A: Se conoce el número de habitantes o se ha calculado en función del número de viviendas. En este caso, el número de habitantes de un edificio es la suma del número de habitantes de todas las viviendas del edificio:

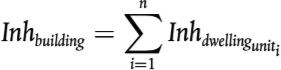
(2.8.1)

1B: El número de habitantes se conoce solo para entidades más grandes que un edificio; por ejemplo, lados de las manzanas, manzanas, secciones censales y distritos o incluso un municipio entero. En este caso, el número de habitantes de un edificio se calcula en función del volumen del edificio:

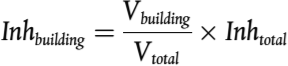
(2.8.2)

El índice aquí hace referencia a la entidad correspondiente considerada. El volumen del edificio es el producto de su superficie construida y de su altura:

(2.8.3)

Si no se conoce la altura del edificio, debe calcularse en función del número de plantas NF_building, suponiendo una altura media por planta de 3 m:

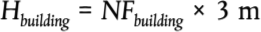
(2.8.4)

Si tampoco se conoce el número de plantas, debe usarse un valor por defecto para el número de plantas representativo del distrito o del municipio.

El volumen total de edificios residenciales de la entidad considerada V_total se calcula como la suma de los volúmenes de todos los edificios residenciales de la entidad:

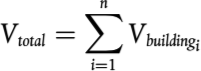
(2.8.5)

CASO 2: no se encuentran disponibles los datos sobre el número de habitantes.

En este caso, el número de habitantes se calcula en función de la superficie de vivienda por habitante FSI. Si no se conoce este parámetro, debe usarse un valor predeterminado nacional.

2A: La superficie residencial útil se conoce en función del número de viviendas. En este caso, el número de habitantes por vivienda se calcula como sigue:

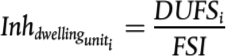
(2.8.6)

El número de habitantes del edificio ahora puede calcularse como en el CASO 1A anterior.

2B: La superficie residencial útil se conoce para todo el edificio, es decir, se conoce la suma de las superficies de todas las viviendas del edificio. En este caso, el número de habitantes se calcula como sigue:

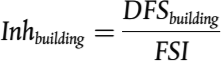
(2.8.7)

2C: La superficie residencial útil se conoce solo para las entidades más grandes que un edificio; por ejemplo, manzanas, secciones censales y distritos o incluso un municipio entero.

En este caso, el número de habitantes de un edificio se calcula en función del volumen del edificio, tal y como se ha descrito en el CASO 1B anterior, donde el número total de habitantes se calcula como sigue:

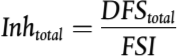
(2.8.8)

2D: Se desconoce la superficie residencial útil. En este caso, el número de habitantes de un edificio se calcula según se ha descrito en el CASO 2B anterior, donde la superficie residencial útil se calcula como sigue:

(2.8.9)

El factor 0,8 es el factor de conversión superficie construida -> superficie útil. Si se conoce un factor diferente como representativo de la superficie, deberá utilizarse y documentarse con claridad.

Si no se conoce el número de plantas del edificio, deberá calcularse en función de la altura del edificio, H_building, cuyo resultado suele ser un número no entero de plantas:

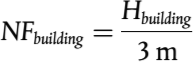
(2.8.10)

Si no se conocen la altura del edificio ni el número de plantas, debe usarse un valor por defecto para el número de plantas representativo del distrito o del municipio.

Asignación de puntos receptores en las fachadas de edificios.

La evaluación de la exposición de la población al ruido se basa en los niveles de ruido en los puntos receptores situados a 4 m por encima del nivel del terreno en las fachadas de los edificios residenciales.

Para calcular el número de habitantes, debe usarse el procedimiento del caso 1 siguiente o el del caso 2 para fuentes de ruido terrestres. En el caso de que el ruido de las aeronaves se calcule según lo indicado en la sección 2.6, se asocia a toda la población de un edificio al punto de cálculo de ruido más próximo de la malla de cálculo.

CASO 1

Figura a

Ejemplo de ubicación de receptores en las fachadas de un edificio, según el procedimiento del CASO 1

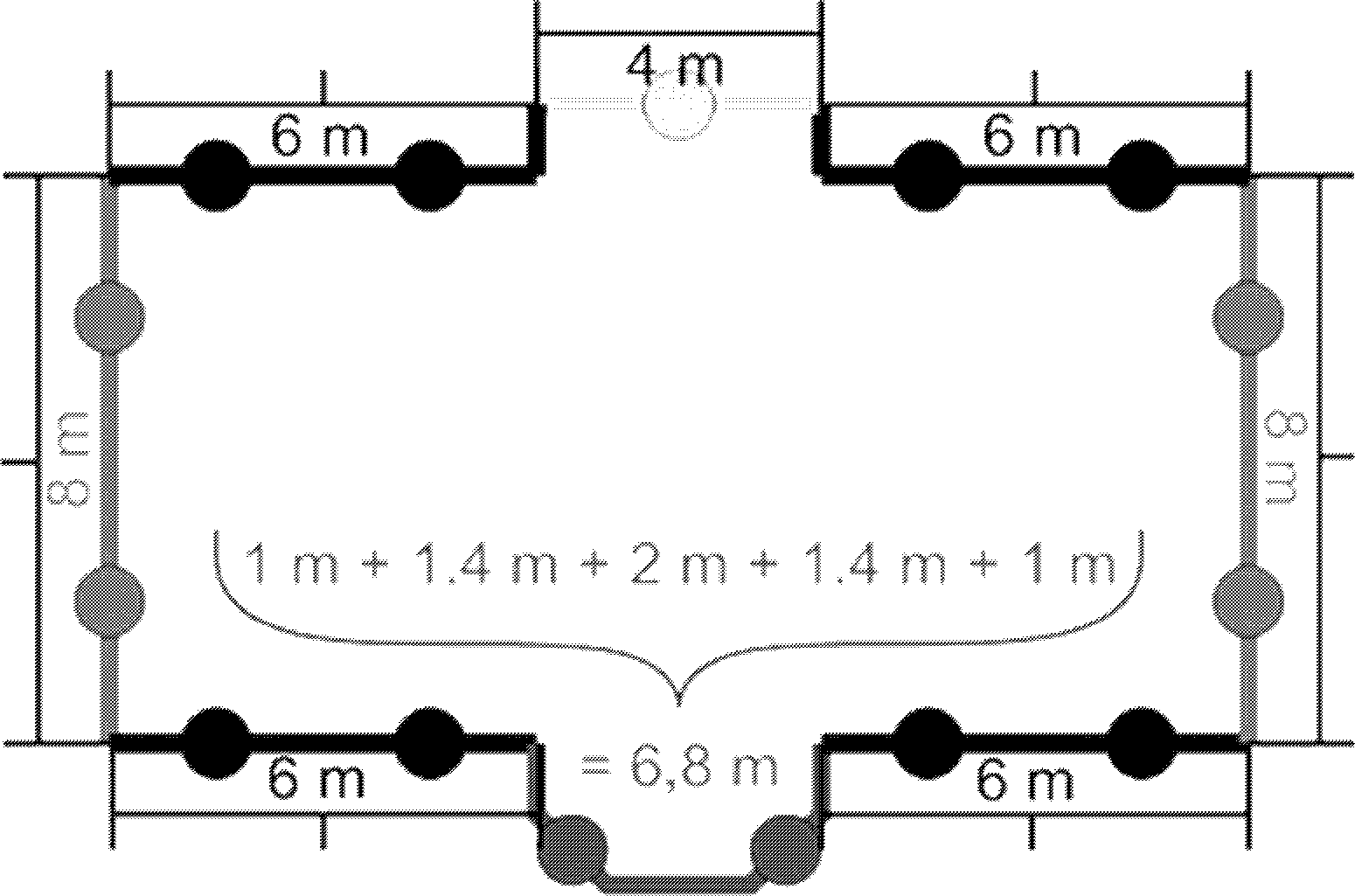
a) Los segmentos con una longitud de más de 5 m se dividen en intervalos regulares de la máxima longitud posible, pero inferior o igual a 5 m. Los puntos receptores se colocan en el medio de cada intervalo regular.

b) Los demás segmentos por encima de una longitud de 2,5 m se representan mediante un punto del receptor en el medio de cada segmento.

c) Los demás segmentos adyacentes con una longitud total de más de 5 m se tratan de manera similar a como se describe en los apartados a) y b).

d) El número de habitantes asignados a un punto receptor debe ponderarse en función de la longitud de la fachada representada, de tal manera que la suma de todos los puntos del receptor represente el número total de habitantes.

e) Solo para los edificios con superficies que indiquen una única vivienda por planta, el nivel de ruido de la fachada más expuesto se usa directamente a efectos estadísticos y está relacionado con el número de habitantes.

CASO 2

Figura b

Ejemplo de ubicación de receptores en las fachadas de un edificio, según el procedimiento del CASO 2

a) Las fachadas se consideran por separado y se dividen cada 5 m desde el punto de partida considerado, con una posición del receptor ubicada a la distancia media de la fachada o del segmento de 5 m.

b) En el último segmento restante, se colocará un punto receptor en su punto medio.

c) El número de habitantes asignados a un punto receptor debe ponderarse en función de la longitud de la fachada representada, de tal manera que la suma de todos los puntos del receptor represente el número total de habitantes.

d) En el caso de edificios con sólo una vivienda por planta, se asigna, a efectos estadísticos, el número de habitantes a la fachada más expuesta.

3. DATOS DE ENTRADA.

Los datos de entrada que se han de utilizar según proceda con los métodos descritos anteriormente se facilitan en los apéndices F a I.

En los casos en que los datos de entrada facilitados en los apéndices F a I no sean aplicables o se desvíen del valor real que no cumplan las condiciones presentadas en las secciones 2.1.2 y 2.6.2, se pueden usar otros valores, siempre que los valores usados y la metodología utilizada para hallarlos estén lo suficientemente documentados, y se demuestre su validez. Esta información se pondrá a disposición del público.

4. MÉTODOS DE MEDICIÓN.

En los casos en que, por algún motivo, se realicen mediciones, estas deberán llevarse a cabo de acuerdo con los principios que rigen las mediciones promedio a largo plazo estipuladas en las normas ISO 1996-1:2003 e ISO 1996-2:2007 o, en el caso del ruido de aeronaves, la ISO 20906:2009.

APÉNDICES

Apéndice A: Requisitos en materia de datos.

Apéndice B: Cálculos de las performances de vuelo.

Apéndice C: Modelización de la extensión de dispersión lateral de la trayectoria en tierra.

Apéndice E: Corrección de segmentos finitos.

Apéndice F: Base de datos para fuentes de tráfico viario.

Apéndice G: Base de datos para fuentes ferroviarias.

Apéndice H: Base de datos para fuentes industriales.

Apéndice I: Base de datos para fuentes asociadas a aeronaves ‒ datos NPD.